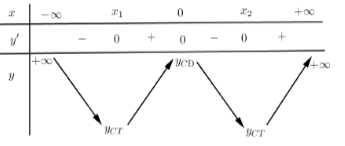
Câu hỏi:
3 năm trước
Cho hàm số \(y = a{x^4} + b{x^2} + c\) có \(a > 0\). Đồ thị hàm số có \(2\) điểm chung với trục hoành nếu:
Trả lời bởi giáo viên
Đáp án đúng: d
+ TH1: \(a > 0,b < 0\), đồ thị có dạng:
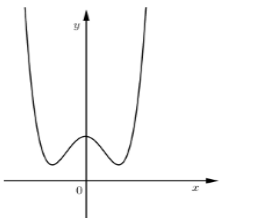
Khi đó, đồ thị hàm số có \(2\) điểm chung với \(Ox\) nếu điểm cực đại \(\left( {0;c} \right)\) nằm hoàn toàn phía dưới \(Ox\) hay \(c < 0\).
Do đó \(c < 0\) .
+TH2: \(a > 0,b \ge 0\), đồ thị có dạng:
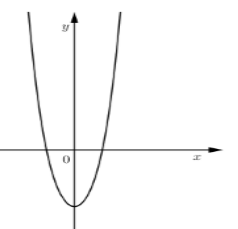
Khi đó, đồ thị hàm số có \(2\) điểm chung với \(Ox\) nếu điểm cực tiểu \(\left( {0;c} \right)\) nằm hoàn toàn phía dưới \(Ox\) hay \(c < 0\).
Vậy trong cả hai trường hợp trên ta đều thấy, nếu \(c < 0\) thì đồ thị hàm số sẽ có hai giao điểm với \(Ox\).
Hướng dẫn giải:
Vẽ dạng đồ thị hàm số bậc bốn trùng phương có \(a > 0\) và tìm điều kiện để đồ thị hàm số có \(2\) điểm chung với trục hoành.