Câu hỏi:
2 năm trước
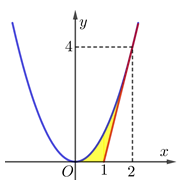
Cho hình phẳng \(\left( H \right)\) giới hạn bởi trục hoành, đồ thị của một parabol và một đường thẳng tiếp xúc parabol đó tại điểm \(A\left( 2;4 \right),\) như hình vẽ bên. Tính thể tích khối tròn xoay tạo bởi hình phẳng \(\left( H \right)\) khi quay xung quanh trục \(Ox.\)
Trả lời bởi giáo viên
Đáp án đúng: b
Vì \(\left( P \right)\) đi qua ba điểm \(O\left( 0;0 \right),\,\,A\left( 2;4 \right)\)
\(\Rightarrow \,\,\) Phương trình parabol là \(\left( P \right):y={{x}^{2}}.\) Tiếp tuyến của \(\left( P \right)\) tại điểm \(A\left( 2;4 \right)\) có phương trình là \(\left( d \right):y=4x-4.\)
Hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là nghiệm phương trình: \({{x}^{2}}=4x-4\Leftrightarrow x=2.\)
Thể tích khối tròn xoay khi quay hình phẳng \(\left( {{H}_{1}} \right)\) giới hạn bởi \(\left( P \right),\,\,y=0,\,\,x=0,\,\,x=2\) là \({{V}_{1}}=\pi \int\limits_{0}^{2}{{{f}^{2}}\left( x \right)\,\text{d}x}=\pi \int\limits_{0}^{2}{{{x}^{4}}\,\text{d}x}=\left. \frac{\pi {{x}^{5}}}{5} \right|_{0}^{2}=\frac{32\pi }{5}.\)
Thể tích khối tròn xoay khi quay hình phẳng \(\left( {{H}_{2}} \right)\) giới hạn bởi \(\left( d \right),\,\,y=0,\,\,x=1,\,\,x=2\) là \({{V}_{2}}=\pi \int\limits_{1}^{2}{{{g}^{2}}\left( x \right)\,\text{d}x}=\pi \int\limits_{1}^{2}{{{\left( 4x-4 \right)}^{2}}\,\text{d}x=}\pi \int\limits_{1}^{2}{16{{\left( x-1 \right)}^{2}}\,\text{d}x=}\left. \frac{16\pi {{\left( x-1 \right)}^{3}}}{3} \right|_{1}^{2}=\frac{16\pi }{3}.\)
Vậy thể tích khối tròn xoay cần tính là \(V={{V}_{1}}-{{V}_{2}}=\frac{32\pi }{5}-\frac{16\pi }{3}=\frac{16\pi }{15}.\)
Hướng dẫn giải:
Chia làm các khối tròn xoay và lấy hiệu
Câu hỏi khác
- Bài tập nguyên hàm toán 12 có lời giải
- Bài tập tích phân các hàm số cơ bản toán 12 có lời giải
- Bài tập tích phân có lời giải MÔN TOÁN Lớp 12
- Bài tập sử dụng phương pháp từng phần để tìm nguyên hàm có lời giải MÔN TOÁN Lớp 12
- Bài tập sử dụng phương pháp đổi biến để tìm nguyên hàm có lời giải MÔN TOÁN Lớp 12
