Câu hỏi:
2 năm trước
Cho tứ diện \(ABCD\) có \(AD = 14,BC = 6\). Gọi \(M,N\) lần lượt là trung điểm của các cạnh \(AC,BD\) và \(MN = 8\). Gọi \(\alpha \) là góc giữa hai đường thẳng \(BC\) và \(MN\). Tính \(\sin \alpha \).
Trả lời bởi giáo viên
Đáp án đúng: b
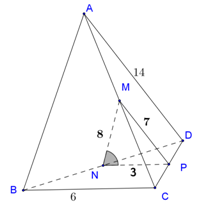
Gọi \(P\) là trung điểm của cạnh \(CD\), ta có \(\alpha = \widehat {\left( {MN,BC} \right)} = \widehat {\left( {MN,NP} \right)}\).
Trong tam giác \(MNP\), ta có \(\cos \widehat {MNP} = \dfrac{{M{N^2} + P{N^2} - M{P^2}}}{{2MN.NP}} = \dfrac{1}{2}\). Suy ra \(\widehat {MNP} = 60^\circ \).
Suy ra \(\sin \alpha = \dfrac{{\sqrt 3 }}{2}\).
Hướng dẫn giải:
- Dựng góc \(\alpha \) bằng cách tìm một đường thẳng song song với \(BC\) mà góc giữa đường thẳng ấy và \(MN\) là dễ nhận thấy.
- Tính góc \(\alpha \) bằng cách sử dụng định lý hàm số \(\cos \)
Câu hỏi khác
- Bài tập thể tích khối chóp toán 12 có lời giải
- Bài tập thể tích lăng trụ, khối hộp toán 12 có lời giải
- Bài tập khối đa diện đều, phép vị tự toán 12 có lời giải
- Bài tập khái niệm về khối đa diện (sự bằng nhau của các khối đa diện) toán 12 có lời giải
- Bài tập khái niệm về khối đa diện toán 12 có lời giải
