Câu hỏi:
2 năm trước
Cho tứ diện đều \(ABCD\) có cạnh bằng $3.$ Gọi \(M,\,N\) lần lượt là trung điểm các cạnh \(AD,\,BD.\) Lấy điểm không đổi \(P\) trên cạnh \(AB\) (khác \(A,\,B\)). Thể tích khối chóp \(P.MNC\) bằng
Trả lời bởi giáo viên
Đáp án đúng: a
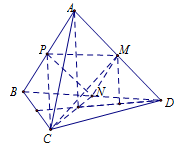
Do \(AB\parallel \left( {CMN} \right)\) nên \(d\left( {P,\,\left( {CMN} \right)} \right) = d\left( {A,\,\left( {CMN} \right)} \right) = d\left( {D,\,\left( {CMN} \right)} \right)\).
Vậy \({V_{PCMN}} = {V_{DMNC}} = {V_{MCND}} = \dfrac{1}{4}{V_{ABCD}}\).
(Do diện tích đáy và chiều cao đều bằng một nửa).
Mặt khác \({V_{ABCD}} = \dfrac{1}{3}\dfrac{{{a^2}\sqrt 3 }}{4}.\sqrt {{a^2} - {{\left( {\dfrac{a}{{\sqrt 3 }}} \right)}^2}} = \dfrac{{{a^3}\sqrt 2 }}{{12}} = \dfrac{{27\sqrt 2 }}{{12}}\) nên \({V_{P.MNC}} = \dfrac{1}{4}.\dfrac{{27\sqrt 2 }}{{12}} = \dfrac{{9\sqrt 2 }}{{16}}\).
Hướng dẫn giải:
So sánh \({V_{PCMN}}\) và \({V_{ABCD}}\) và tính thể tích \({V_{ABCD}}\) rồi suy ra kết luận.
Câu hỏi khác
- Bài tập thể tích khối chóp toán 12 có lời giải
- Bài tập thể tích lăng trụ, khối hộp toán 12 có lời giải
- Bài tập khối đa diện đều, phép vị tự toán 12 có lời giải
- Bài tập khái niệm về khối đa diện (sự bằng nhau của các khối đa diện) toán 12 có lời giải
- Bài tập khái niệm về khối đa diện toán 12 có lời giải
