Câu hỏi:
2 năm trước
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi tâm $O$, $AB = a$, $\widehat {BAD} = 60^\circ $, $SO \bot \left( {ABCD} \right)$ và mặt phẳng $\left( {SCD} \right)$ tạo với mặt đáy một góc $60^\circ $. Tính thể tích khối chóp $S.ABCD$
Trả lời bởi giáo viên
Đáp án đúng: b
${S_{ABCD}} = 2{S_{ABD}} = AB.AD.\sin \widehat {BAD} = a.a.\sin 60^\circ = \dfrac{{{a^2}\sqrt 3 }}{2}$
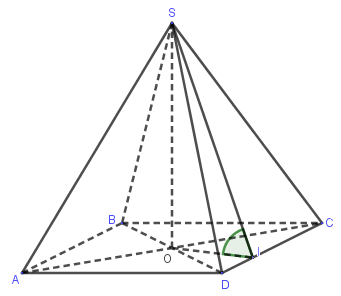
Trong $\left( {ABCD} \right)$, dựng $OI \bot CD$.
Ta có $\left. \begin{array}{l}CD \bot OI\\CD \bot SO\end{array} \right\} \Rightarrow CD \bot \left( {SOI} \right) \Rightarrow CD \bot SI$
Do đó, $\left( {\left( {SCD} \right),\left( {ABCD} \right)} \right) = \left( {SI,OI} \right) = \widehat {SIO} = 60^\circ $
Tam giác $OCI$ vuông tại $I$ nên
$\sin \widehat {OCI} = \dfrac{{OI}}{{OC}} \Leftrightarrow OI = OC.\sin \widehat {OCI} = \dfrac{{a\sqrt 3 }}{2}.\sin 30^\circ = \dfrac{{a\sqrt 3 }}{4}$
Tam giác $SOI$ vuông tại $O$ nên $\tan \widehat {SIO} = \dfrac{{SO}}{{OI}} \Rightarrow SO = OI.\tan \widehat {SIO} = \dfrac{{a\sqrt 3 }}{4}.\tan 60^\circ = \dfrac{{3a}}{4}$
Vậy ${V_{S.ABCD}} = \dfrac{1}{3}{S_{ABCD}}.SO = \dfrac{1}{3}.\dfrac{{{a^2}\sqrt 3 }}{2}.\dfrac{{3a}}{4} = \dfrac{{{a^3}\sqrt 3 }}{8}$
Hướng dẫn giải:
- Xác định góc giữa \(\left( {SCD} \right)\) và \(ABCD\) (là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến \(CD\))
- Tính \(SO\) và \({S_{ABCD}}\) rồi tính thể tích khối chóp theo công thức \(V = \dfrac{1}{3}Sh\)
Câu hỏi khác
- Bài tập thể tích khối chóp toán 12 có lời giải
- Bài tập thể tích lăng trụ, khối hộp toán 12 có lời giải
- Bài tập khối đa diện đều, phép vị tự toán 12 có lời giải
- Bài tập khái niệm về khối đa diện (sự bằng nhau của các khối đa diện) toán 12 có lời giải
- Bài tập khái niệm về khối đa diện toán 12 có lời giải
