Câu hỏi:
2 năm trước
Cho lăng trụ tam giác \(ABC.A'B'C'\) có đáy \(ABC\) là đều cạnh \(AB = 2a\sqrt 2 \). Biết \(AC' = 8a\) và tạo với mặt đáy một góc \({45^0}\). Thể tích khối đa diện \(ABCC'B'\) bằng
Trả lời bởi giáo viên
Đáp án đúng: d
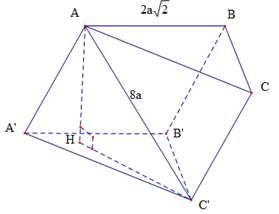
Gọi \(H\) là hình chiếu của \(A\) lên \(mp\left( {A'B'C'} \right)\).
\( \Rightarrow \widehat {HC'A} = {45^0}\).
\( \Rightarrow \Delta AHC'\) vuông cân tại $H.$
\( \Rightarrow AH = AC'.\sin 45^0=AC'.\dfrac{{\sqrt 2}}{{2}} = 4a\sqrt 2 .\)
Diện tích tam giác $ABC$ là: $S_{ABC}=\dfrac{(2a\sqrt{2})^2\sqrt{3}}{4}$
NX: \({V_{A.BCC'B'}} = \dfrac{2}{3}{V_{ABC.A'B'C'}} = \dfrac{2}{3}AH.{S_{ABC}} = \dfrac{2}{3}.4a\sqrt 2 .\dfrac{{{{\left( {2a\sqrt 2 } \right)}^2}.\sqrt 3 }}{4} = \dfrac{{16{a^3}\sqrt 6 }}{3}.\)
Hướng dẫn giải:
- Tính thể tích khối lăng trụ \(ABC.A'B'C'\) theo công thức \(V = Bh\) với \(B\) là diện tích đáy, \(h\) là chiều cao.
- Tính thể tích khối lăng trụ \({V_{ABCC'B'}}\) với chú ý \({V_{ABCC'B'}} = \dfrac{2}{3}{V_{ABC.A'B'C'}}\)
- Công thức tính diện tích tam giác đều cạnh $a$.
$S=\dfrac{a^2\sqrt{3}}{4}$
Câu hỏi khác
- Bài tập thể tích khối chóp toán 12 có lời giải
- Bài tập thể tích lăng trụ, khối hộp toán 12 có lời giải
- Bài tập khối đa diện đều, phép vị tự toán 12 có lời giải
- Bài tập khái niệm về khối đa diện (sự bằng nhau của các khối đa diện) toán 12 có lời giải
- Bài tập khái niệm về khối đa diện toán 12 có lời giải
