Cho khối chóp \(S.ABCD\) có thể tích bằng \(16\). Gọi \(M\), \(N\), \(P\), \(Q\) lần lượt là trung điểm của \(SA\), \(SB\), \(SC\), \(SD\). Tính thể tích khối chóp \(S.MNPQ\).
Ta có: \(\dfrac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = \dfrac{{SM}}{{SA}}.\dfrac{{SN}}{{SB}}.\dfrac{{SP}}{{SC}} = \dfrac{1}{8}\), \(\dfrac{{{V_{S.MQP}}}}{{{V_{S.ADC}}}} = \dfrac{{SM}}{{SA}}.\dfrac{{SQ}}{{SD}}.\dfrac{{SP}}{{SC}} = \dfrac{1}{8}\).
Ta có: $\dfrac{1}{8} = \dfrac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = \dfrac{{{V_{S.MQP}}}}{{{V_{S.ADC}}}} = \dfrac{{{V_{S.MNP}} + {V_{S.MQP}}}}{{{V_{S.ABC}} + {V_{S.ADC}}}} = \dfrac{{{V_{S.MNPQ}}}}{{{V_{S.ABCD}}}}$.
\( \Rightarrow {V_{S.MNPQ}} = 2\).
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân, \(AB = AC = a\), \(SC \bot \left( {ABC} \right)\) và \(SC = a\). Mặt phẳng qua \(C\), vuông góc với \(SB\) cắt \(SA,SB\) lần lượt tại \(E\) và \(F\). Tính thể tích khối chóp \(S.CEF\).
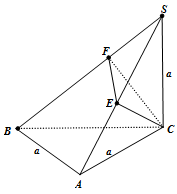
Từ \(C\) hạ \(CF \bot SB,\left( {F \in SB} \right)\), \(CE \bot SA,\left( {E \in SA} \right)\)
Ta có:\(\begin{array}{l}\left\{ \begin{array}{l}AB \bot AC\\AB \bot SC\end{array} \right. \Rightarrow AB \bot \left( {SAC} \right) \Rightarrow AB \bot CE\\ \Rightarrow CE \bot \left( {SAB} \right) \Rightarrow CE \bot SB\end{array}\)
Vậy mặt phẳng qua \(C\) và vuông góc \(SB\) là mặt \(\left( {CEF} \right)\)
Ta có \(\dfrac{{{V_{SCEF}}}}{{{V_{SCAB}}}} = \dfrac{{SE}}{{SA}}.\dfrac{{SF}}{{SB}}\)
Tam giác vuông \(SAC\) vuông tại \(C\) ta có:
\(SA = \sqrt {S{C^2} + A{C^2}} = a\sqrt 2 \) và \(\dfrac{{SE}}{{SA}} = \dfrac{{S{C^2}}}{{S{A^2}}} = \dfrac{{{a^2}}}{{2{a^2}}} \Rightarrow \dfrac{{SE}}{{SA}} = \dfrac{1}{2}\)
Tam giác vuông \(SBC\) vuông tại \(C\) ta có:
\(SB = \sqrt {S{C^2} + B{C^2}} = a\sqrt 3 \) và \(\dfrac{{SF}}{{SB}} = \dfrac{{S{C^2}}}{{S{B^2}}} = \dfrac{{{a^2}}}{{3{a^2}}} \Rightarrow \dfrac{{SF}}{{SB}} = \dfrac{1}{3}\)
Do đó: \(\dfrac{{{V_{SCEF}}}}{{{V_{SCAB}}}} = \dfrac{1}{2}.\dfrac{1}{3} = \dfrac{1}{6} \Rightarrow {V_{SCEF}} = \dfrac{1}{6}{V_{SABC}} = \dfrac{1}{6}.\dfrac{1}{3}SC.{S_{ABC}} = \dfrac{1}{{36}}{a^3}\)
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh $a$, hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAD} \right)\) cùng vuông góc với đáy, biết \(SC = a\sqrt 3 \). Gọi \(M,\)\(N,\)\(P,\)\(Q\) lần lượt là trung điểm của \(SB,\)\(SD,\)\(CD,\)\(BC\). Tính thể tích của khối chóp \(A.MNPQ\).
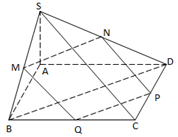
Có: \(\left\{ \begin{array}{l}MN//PQ\\MN = PQ\\NP \bot PQ\left( {BD \bot SC} \right)\end{array} \right.\)
Vậy \(MNPQ\) là hình chữ nhật.
Suy ra:
\({V_{A.MNPQ}} = 2{V_{A.MQP}} = 2{V_{M.AQP}} \) \(= 2.\dfrac{1}{3}{S_{AQP}}.d\left( {M,\left( {AQP} \right)} \right)\) \(= \dfrac{2}{3}{S_{AQP}}.\dfrac{1}{2}SA\)
Có: \(SA = \sqrt {S{C^2} - A{C^2}} = a\)
Với \({S_{AQP}} = \dfrac{1}{2}.\dfrac{3}{4}AC.\dfrac{1}{2}BD = \dfrac{3}{{16}}{\left( {a\sqrt 2 } \right)^2} = \dfrac{3}{8}{a^2}\)
Vậy \({V_{A.MNPQ}} = \dfrac{1}{3}.\dfrac{{3{a^2}}}{8}.a = \dfrac{{{a^3}}}{8}.\)
Một lăng trụ đứng tam giác có các cạnh đáy là $11\,cm$, $12\,cm$, $13\,cm$ và diện tích xung quanh bằng $144\,c{m^2}$. Thể tích của khối lăng trụ đó là:
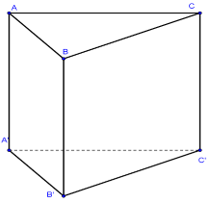
Ta có: \({S_{xq}} = \left( {11 + 12 + 13} \right)h = 144 \) \(\Rightarrow h = \dfrac{{144}}{{36}} = 4\)
Diện tích đáy: ${S_d} = \sqrt {18\left( {18 - 11} \right)\left( {18 - 12} \right)\left( {18 - 13} \right)} = 6\sqrt {105} $
Vậy thể tích khối lăng trụ: $V = {S_d}.h = 24\sqrt {105} \,c{m^3}$
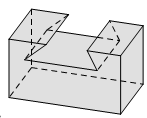
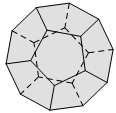
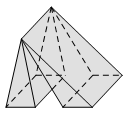
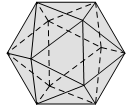
Vật thể nào trong các vật thể sau không phải là khối đa diện?
Vì hình C vi phạm tính chất “Mỗi cạnh của miền đa giác nào cũng là cạnh chung của đúng hai miền đa giác”.
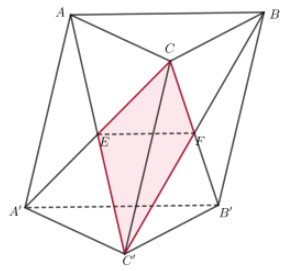
Cho khối lăng trụ tam giác đều ABC.A′B′C′. Các mặt phẳng (ABC′) và (A′B′C) chia khối lăng trụ đã cho thành 4 khối đa diện. Kí hiệu H1, H2 lần lượt là khối có thể tích lớn nhất và nhỏ nhất trong bốn khối trên. Giá trị của \(\dfrac{{{V_{\left( {{H_1}} \right)}}}}{{{V_{\left( {{H_2}} \right)}}}}\) bằng
 s
s
Bước 1:
Gọi \(E\) là giao điểm của AC và AC’ và F là giao điểm của BC’ và B’C’
Khi đó (ABC’) và (A’B’C) chia khối lăng trụ tam giác đều ABC.A’B’C’ thành 4 khối đa diện: CEFC’;FEA’B’C’;FEABC và FEABB’A’
Gọi V là thể tích của khối lăng trụ tam giác đều ABC.A’B’C’.
Bước 2: Tính thể tích của $CEFC’;FEA’B’C’;FEABC$ và $FEABB’A'$ theo thể tích của $ABC.A'B'C'$
Ta có \({V_{C.A'B'C'}} = {V_{C'.ABC}} = \dfrac{1}{3}V\)
\({V_{FEA'B'C'}} = {V_{C.A'B'C'}} - {V_{CEFC'}}\) và \({V_{FEABC}} = {V_{C'.ABC}} - {V_{CEFC'}}\)
\( \Rightarrow {V_{FEA'B'C'}} = {V_{FEABC}}\)
Mặt khác
\(\begin{array}{l}\dfrac{{{V_{CEFC'}}}}{{V_{C.A'B'C'}}} = \dfrac{{CE}}{{CA}}.\dfrac{{CF}}{{CB'}} = \dfrac{1}{2}.\dfrac{1}{2} = \dfrac{1}{4}\\ \Rightarrow {V_{CEFC'}} = \dfrac{1}{4}{V_{C.A'B'C'}} = \dfrac{1}{4}.\dfrac{1}{3}V = \dfrac{1}{{12}}V\end{array}\)
\( \Rightarrow {V_{FEA'B'C'}} = {V_{FEABC}}\)\( = {V_{C.A'B'C'}} - {V_{CEFC'}}\)\( = \dfrac{1}{3}V - \dfrac{1}{{12}}V = \dfrac{1}{4}V\)
\( \Rightarrow {V_{FEABB'A'}} = V - 2.\dfrac{1}{4}V - \dfrac{1}{{12}}V = \dfrac{5}{{12}}V\)
Do đó \({H_1}\) có thể tích lớn nhất là khối đa diện FEABB’A’; \({H_2}\) có thể tích nhỏ nhất là khối đa diện CEFC’ và \(\dfrac{{{V_{\left( {{H_1}} \right)}}}}{{{V_{\left( {{H_2}} \right)}}}} = 5\).