Cho khối lăng trụ tam giác đều ABC.A′B′C′. Các mặt phẳng (ABC′) và (A′B′C) chia khối lăng trụ đã cho thành 4 khối đa diện. Kí hiệu H1, H2 lần lượt là khối có thể tích lớn nhất và nhỏ nhất trong bốn khối trên. Giá trị của \(\dfrac{{{V_{\left( {{H_1}} \right)}}}}{{{V_{\left( {{H_2}} \right)}}}}\) bằng

s

Bước 1: 

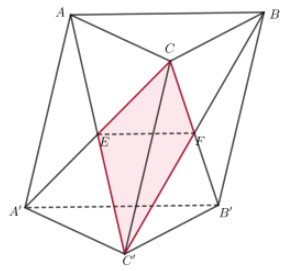
Gọi \(E\) là giao điểm của AC và AC’ và F là giao điểm của BC’ và B’C’

Khi đó (ABC’) và (A’B’C) chia khối lăng trụ tam giác đều ABC.A’B’C’ thành 4 khối đa diện: CEFC’;FEA’B’C’;FEABC và FEABB’A’

Gọi V là thể tích của khối lăng trụ tam giác đều ABC.A’B’C’.

Bước 2: Tính thể tích của $CEFC’;FEA’B’C’;FEABC$ và $FEABB’A'$ theo thể tích của $ABC.A'B'C'$

Ta có \({V_{C.A'B'C'}} = {V_{C'.ABC}} = \dfrac{1}{3}V\)

\({V_{FEA'B'C'}} = {V_{C.A'B'C'}} - {V_{CEFC'}}\) và \({V_{FEABC}} = {V_{C'.ABC}} - {V_{CEFC'}}\)

\( \Rightarrow {V_{FEA'B'C'}} = {V_{FEABC}}\)

Mặt khác

\(\begin{array}{l}\dfrac{{{V_{CEFC'}}}}{{V_{C.A'B'C'}}} = \dfrac{{CE}}{{CA}}.\dfrac{{CF}}{{CB'}} = \dfrac{1}{2}.\dfrac{1}{2} = \dfrac{1}{4}\\ \Rightarrow {V_{CEFC'}} = \dfrac{1}{4}{V_{C.A'B'C'}} = \dfrac{1}{4}.\dfrac{1}{3}V = \dfrac{1}{{12}}V\end{array}\)

\( \Rightarrow {V_{FEA'B'C'}} = {V_{FEABC}}\)\( = {V_{C.A'B'C'}} - {V_{CEFC'}}\)\( = \dfrac{1}{3}V - \dfrac{1}{{12}}V = \dfrac{1}{4}V\)

\( \Rightarrow {V_{FEABB'A'}} = V - 2.\dfrac{1}{4}V - \dfrac{1}{{12}}V = \dfrac{5}{{12}}V\)

Do đó \({H_1}\) có thể tích lớn nhất là khối đa diện FEABB’A’; \({H_2}\) có thể tích nhỏ nhất là khối đa diện CEFC’ và \(\dfrac{{{V_{\left( {{H_1}} \right)}}}}{{{V_{\left( {{H_2}} \right)}}}} = 5\).