Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh $a$, hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAD} \right)\) cùng vuông góc với đáy, biết \(SC = a\sqrt 3 \). Gọi \(M,\)\(N,\)\(P,\)\(Q\) lần lượt là trung điểm của \(SB,\)\(SD,\)\(CD,\)\(BC\). Tính thể tích của khối chóp \(A.MNPQ\).
Trả lời bởi giáo viên
Đáp án đúng: b
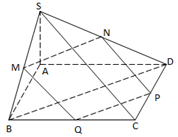
Có: \(\left\{ \begin{array}{l}MN//PQ\\MN = PQ\\NP \bot PQ\left( {BD \bot SC} \right)\end{array} \right.\)
Vậy \(MNPQ\) là hình chữ nhật.
Suy ra:
\({V_{A.MNPQ}} = 2{V_{A.MQP}} = 2{V_{M.AQP}} \) \(= 2.\dfrac{1}{3}{S_{AQP}}.d\left( {M,\left( {AQP} \right)} \right)\) \(= \dfrac{2}{3}{S_{AQP}}.\dfrac{1}{2}SA\)
Có: \(SA = \sqrt {S{C^2} - A{C^2}} = a\)
Với \({S_{AQP}} = \dfrac{1}{2}.\dfrac{3}{4}AC.\dfrac{1}{2}BD = \dfrac{3}{{16}}{\left( {a\sqrt 2 } \right)^2} = \dfrac{3}{8}{a^2}\)
Vậy \({V_{A.MNPQ}} = \dfrac{1}{3}.\dfrac{{3{a^2}}}{8}.a = \dfrac{{{a^3}}}{8}.\)
Hướng dẫn giải:
- Nhận xét thể tích khối chóp \(A.MNPQ\) so với thể tích khối chóp \(A.MPQ\)
- Tính thể tích \({V_{A.MPQ}}\) và suy ra kết luận.
Câu hỏi khác
- Bài tập thể tích khối chóp toán 12 có lời giải
- Bài tập thể tích lăng trụ, khối hộp toán 12 có lời giải
- Bài tập khối đa diện đều, phép vị tự toán 12 có lời giải
- Bài tập khái niệm về khối đa diện (sự bằng nhau của các khối đa diện) toán 12 có lời giải
- Bài tập khái niệm về khối đa diện toán 12 có lời giải
