Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân, \(AB = AC = a\), \(SC \bot \left( {ABC} \right)\) và \(SC = a\). Mặt phẳng qua \(C\), vuông góc với \(SB\) cắt \(SA,SB\) lần lượt tại \(E\) và \(F\). Tính thể tích khối chóp \(S.CEF\).

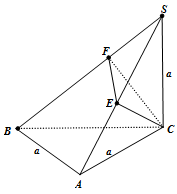
Từ \(C\) hạ \(CF \bot SB,\left( {F \in SB} \right)\), \(CE \bot SA,\left( {E \in SA} \right)\)

Ta có:\(\begin{array}{l}\left\{ \begin{array}{l}AB \bot AC\\AB \bot SC\end{array} \right. \Rightarrow AB \bot \left( {SAC} \right) \Rightarrow AB \bot CE\\ \Rightarrow CE \bot \left( {SAB} \right) \Rightarrow CE \bot SB\end{array}\)

Vậy mặt phẳng qua \(C\) và vuông góc \(SB\) là mặt \(\left( {CEF} \right)\)

Ta có \(\dfrac{{{V_{SCEF}}}}{{{V_{SCAB}}}} = \dfrac{{SE}}{{SA}}.\dfrac{{SF}}{{SB}}\)

Tam giác vuông \(SAC\) vuông tại \(C\) ta có:

\(SA = \sqrt {S{C^2} + A{C^2}}  = a\sqrt 2 \) và \(\dfrac{{SE}}{{SA}} = \dfrac{{S{C^2}}}{{S{A^2}}} = \dfrac{{{a^2}}}{{2{a^2}}} \Rightarrow \dfrac{{SE}}{{SA}} = \dfrac{1}{2}\)

Tam giác vuông \(SBC\) vuông tại \(C\) ta có:

\(SB = \sqrt {S{C^2} + B{C^2}}  = a\sqrt 3 \) và \(\dfrac{{SF}}{{SB}} = \dfrac{{S{C^2}}}{{S{B^2}}} = \dfrac{{{a^2}}}{{3{a^2}}} \Rightarrow \dfrac{{SF}}{{SB}} = \dfrac{1}{3}\)

Do đó: \(\dfrac{{{V_{SCEF}}}}{{{V_{SCAB}}}} = \dfrac{1}{2}.\dfrac{1}{3} = \dfrac{1}{6} \Rightarrow {V_{SCEF}} = \dfrac{1}{6}{V_{SABC}} = \dfrac{1}{6}.\dfrac{1}{3}SC.{S_{ABC}} = \dfrac{1}{{36}}{a^3}\)