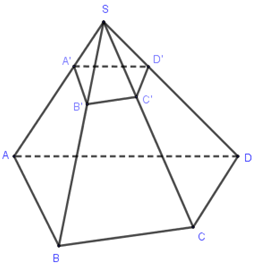
Cho hình chóp tứ giác \(S.ABCD\). Gọi \(V\) là thể tích khối chóp \(S.ABCD\). Lấy điểm \(A'\) trên cạnh \(SA\)sao cho \(SA = 4SA'\). Mặt phẳng qua \(A'\) và song song với đáy của hình chóp cắt các cạnh \(SB\), \(SC\), \(SD\) lần lượt tại các điểm \(B'\), \(C'\), \(D'\). Thể tích khối chóp \(S.A'B'C'D'\)bằng:

Bát diện đều có mấy đỉnh ?

Cho khối chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\), \(SA \bot \left( {ABC} \right)\) và \(SA = a\). Tính thể tích khối chóp \(S.ABC\).

Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(C,\)\(AB = a\sqrt 5 ,\)\(AC = a.\) Cạnh bên \(SA = 3a\) và vuông góc với mặt phẳng đáy. Thể tích của khối chóp \(S.ABC\) bằng

Cho hình chóp \(S.ABC\) có đáy là tam giác đều cạnh \(2a\) và thể tích bằng \({a^3}\). Tính chiều cao \(h\) của hình chóp đã cho.

Cho tứ diện \(ABCD\) có thể tích bằng $12$ và \(G\) là trọng tâm tam giác \(BCD\). Tính thể tích \(V\) của khối chóp \(A.GBC\).

Cho tứ diện \(ABCD\) có \(AD = 14,BC = 6\). Gọi \(M,N\) lần lượt là trung điểm của các cạnh \(AC,BD\) và \(MN = 8\). Gọi \(\alpha \) là góc giữa hai đường thẳng \(BC\) và \(MN\). Tính \(\sin \alpha \).

Cho hình chóp tứ giác $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, \(SA \bot (ABCD)\) và \(SA = a\sqrt 6 \). Thể tích của khối chóp $S.ABCD$ bằng