Câu hỏi:
2 năm trước
Cho hình lăng trụ \(ABC.A'B'C'\) có thể tích bằng \(V\). Các điểm \(M\), \(N\), \(P\) lần lượt thuộc các cạnh $AA'$, $BB'$, $CC'$ sao cho $\dfrac{{AM}}{{AA'}} = \dfrac{1}{2}$, $\dfrac{{BN}}{{BB'}} = \dfrac{{CP}}{{CC'}} = \dfrac{2}{3}$. Thể tích khối đa diện \(ABC.MNP\) bằng
Trả lời bởi giáo viên
Đáp án đúng: d
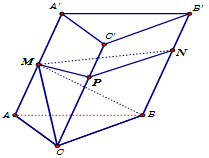
Có ${V_{A'.B'C'CB}} = \dfrac{2}{3}V = {V_{M.B'C'CB}}$
Đặt: ${V_1} = {V_{M.NPCB}} = \dfrac{1}{3}d\left( {M,\left( {CC'B'B} \right)} \right).{S_{NPCB}}$
$ = \dfrac{1}{3}d\left( {M,\left( {CC'B'B} \right)} \right).\dfrac{2}{3}{S_{CC'B'B}}$ $ = \dfrac{2}{3}.\dfrac{1}{3}d\left( {M,\left( {CC'B'B} \right)} \right).{S_{CC'B'B}} $ $= \dfrac{2}{3}{V_{M.CC'B'B}} = \dfrac{2}{3}.\dfrac{2}{3}.V = \dfrac{4}{9}V$
$\begin{array}{l}{V_2} = {V_{M.ABC}} = \dfrac{1}{3}d\left( {M,\left( {ABC} \right)} \right).{S_{ABC}}\\ = \dfrac{1}{3}.\dfrac{1}{2}d\left( {A',\left( {ABC} \right)} \right).{S_{ABC}} = \dfrac{1}{6}V\end{array}$
Vậy \({V_{ABC.MNP}} = {V_1} + {V_2} = \dfrac{4}{9}V + \dfrac{1}{6}V = \dfrac{{11}}{{18}}V\)
Hướng dẫn giải:
Tính tỉ số thể tích các khối chóp \(M.NPCB\) và \(M.ABC\) so với thể tích khối lăng trụ \(ABC.A'B'C'\) và suy ra kết luận.
Câu hỏi khác
- Bài tập thể tích khối chóp toán 12 có lời giải
- Bài tập thể tích lăng trụ, khối hộp toán 12 có lời giải
- Bài tập khối đa diện đều, phép vị tự toán 12 có lời giải
- Bài tập khái niệm về khối đa diện (sự bằng nhau của các khối đa diện) toán 12 có lời giải
- Bài tập khái niệm về khối đa diện toán 12 có lời giải
