Câu hỏi:
2 năm trước
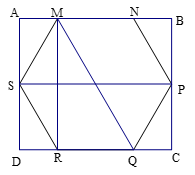
Cho một cây nến hình lăng trụ lục giác đều có chiều cao và độ dài cạnh đáy lần lượt là \(15{\rm{cm}}\) và \(5{\rm{cm}}\). Người ta xếp cây nến trên vào trong một hộp có dạng hình hộp chữ nhật sao cho cây nến nằm khít trong hộp ( có đáy tiếp xúc như hình vẽ). Thể tích của chiếc hộp đó bằng.
Trả lời bởi giáo viên
Đáp án đúng: d
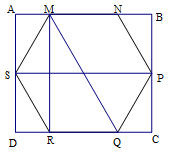
Ta có \(AB = SP = 2MN = 10cm\).
\(AD = MR = 2.\sqrt {{5^2} - {{\left( {\dfrac{5}{2}} \right)}^2}} = 5\sqrt 3 \)
\( \Rightarrow {S_{ABCD}} = AB.AD = 50\sqrt 3 \,\,c{m^2}\).
$V = {S_{ABCD}}.h = 50\sqrt 3 .15 = 750\sqrt 3 \,c{m^3}$.
Hướng dẫn giải:
Tính diện tích đáy hộp \({S_{ABCD}}\) rồi sử dụng công thức tính thể tích khối lăng trụ \(V = Sh\) với \(S\) là diện tích đáy, \(h\) là chiều cao.

