Tìm m để tồn tại duy nhất cặp (x;y) thỏa mãn logx2+y2+2(4x+4y−4)≥1 và x2+y2+2x−2y+2−m=0.
Trả lời bởi giáo viên
Điều kiện 4x+4y−4>0
Ta có logx2+y2+2(4x+4y−4)≥1 ⇔4x+4y−4≥x2+y2+2⇔(x−2)2+(y−2)2≤2(C1)
Miền nghiệm của bất phương trình là hình tròn (cả bờ) (C1) có tâm I1(2;2) bán kính R1=√2
Mặt khác: x2+y2+2x−2y+2−m=0⇔(x+1)2+(y−1)2=m(∗)
Với m=0 ⇒x=−1;y=1 không thỏa mãn: (x−2)2+(y−2)2≤2.
Với m>0 thì (∗) là đường tròn(C2) có tâm I2(−1;1) bán kính R2=√m.
Để tồn tại duy nhất cặp (x;y) thì (C1) và (C2) tiếp xúc với nhau.
Trường hợp 1: (C1) và(C2) tiếp xúc ngoài.
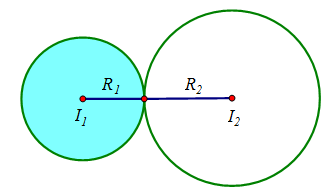
Khi đó: R1+R2=I1I2⇔√m+√2=√10⇔m=(√10−√2)2
Trường hợp 2: (C1) nằm trong (C2) và hai đường tròn tiếp xúc trong.
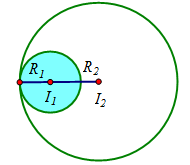
Khi đó: R2−R1=I1I2⇔√m−√2=√10 ⇔m=(√10+√2)2
Vậy m=(√10−√2)2 và m=(√10+√2)2 thỏa mãn yêu cầu bài toán.
Hướng dẫn giải:
- Tìm miền nghiệm của bất phương trình đầu.
- Biện luận tập nghiệm của phương trình sau theo các trường hợp của m
- Dùng minh họa hình học để tìm điều kiện tồn tại duy nhất cặp (x;y) thỏa mãn.

