Cho phương trình 4 \({4^{ - |x - m|}} \cdot {\log _{\sqrt 2 }}\left( {{x^2} - 2x + 3} \right) + {2^{2x - {x^2}}} \cdot {\log _{\frac{1}{2}}}(2|x - m| + 2) = 0\) với \(m\) là tham số. Tổng tất cả các giá trị của tham số m để phương trình đã cho có ba nghiệm phân biệt là

Bước 1: Biến đổi phương trình để đưa về dạng xét hàm đặc trưng

Phương trình đã cho tương đương với phương trình

\({2^{ - 2}}|x - m| + 1 \cdot {\log _2}\left( {{x^2} - 2x + 3} \right)\)\( - {2^{2x - {x^2}}} \cdot {\log _2}(2|x - m| + 2) = 0\) \( \Leftrightarrow {2^{ - 2}}|x - m| + 1 \cdot {\log _2}\left( {{x^2} - 2x + 3} \right)\)\( = {2^{2x - {x^2}}} \cdot {\log _2}(2|x - m| + 2)\)

\( \Leftrightarrow {2^{{x^2} - 2x}} \cdot {\log _2}\left( {{x^2} - 2x + 3} \right)\)\( = {2^2}|x - m| - 1 \cdot {\log _2}(2|x - m| + 2)\)

Bước 2: Xét hàm đặc trưng \(f(t) = {2^{t - 3}} \cdot {\log _2}t\) với \(t \ge 2\) rồi cô lập m, \(m = g\left( x \right)\)

Xét hàm số \(f(t) = {2^{t - 3}} \cdot {\log _2}t\) với \(t \ge 2\). Do \(t \ge 2\) suy ra \({\log _2}t \ge 1\).

Ta có: \({f^\prime }(t) = {2^{t - 3}} \cdot \dfrac{1}{{t.\ln 2}} + {2^{t - 3}} \cdot \ln 2 \cdot {\log _2}t > 0\) với \(t \ge 2\).

Do đó hàm số \(f(t)\) đồng biến trên \([2; + \infty )\)

\( \Rightarrow f\left( {{x^2} - 2x + 3} \right) = f(2|x - m| + 2)\)\( \Leftrightarrow {x^2} - 2x + 3 = 2|x - m| + 2\)\( \Leftrightarrow |x - m| = \dfrac{{{x^2}}}{2} - x + \dfrac{1}{2}\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = \dfrac{{ - {x^2}}}{2} + 2x - \dfrac{1}{2}}\\{m = \dfrac{{{x^2}}}{2} + \dfrac{1}{2}}\end{array}(*)} \right.\)

Bước 3: Tìm tổng các giá trị m để phương trình có 3 nghiệm

Vẽ đồ thị các hàm số \(y = \dfrac{{ - {x^2}}}{2} + 2x - \dfrac{1}{2}\) và \(y = \dfrac{{{x^2}}}{2} + \dfrac{1}{2}\) trên cùng một hệ trục tọa độ.

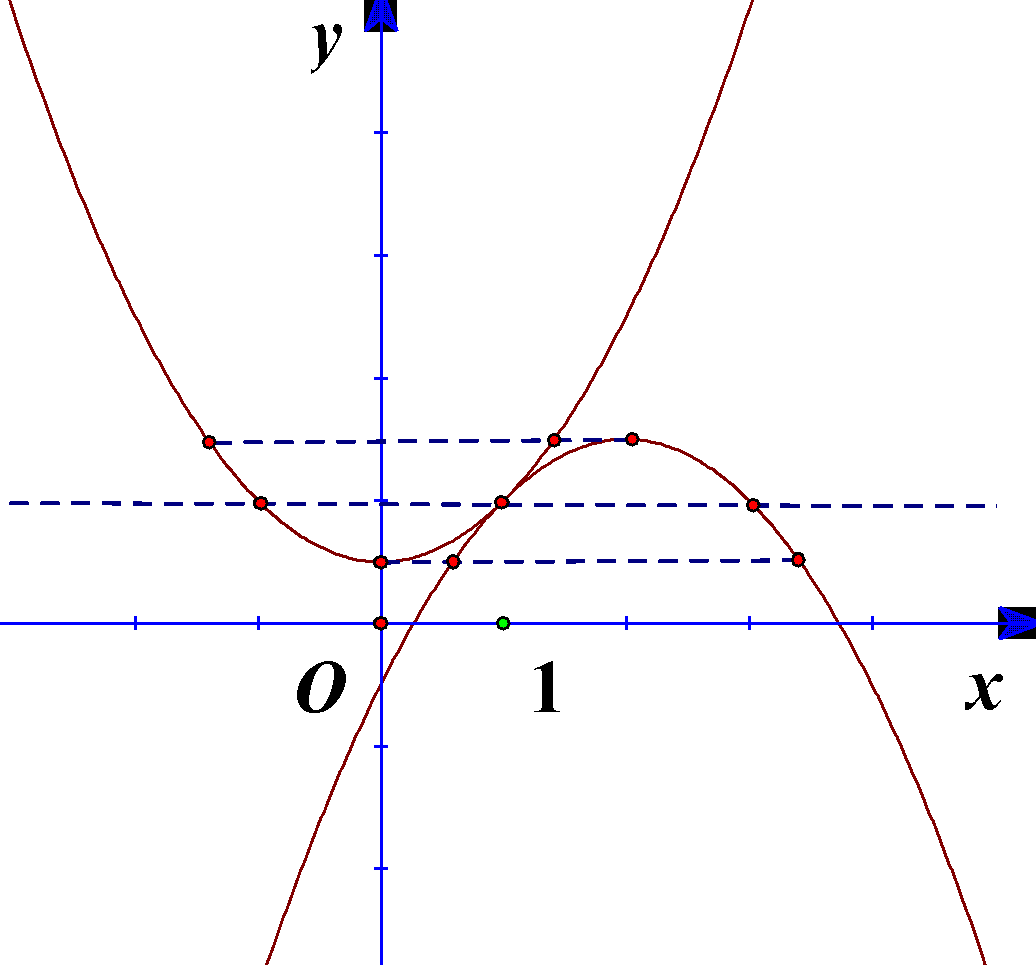
Đồ thị hai hàm số tiếp xúc với nhau tại điểm \((1;1)\). Điểm cực trị của đồ thị hàm số \(y = \dfrac{{{x^2}}}{2} + \dfrac{1}{2}\) là \(\left( {0;\dfrac{1}{2}} \right)\), điểm cực trị của đồ thị hàm số \(y = \dfrac{{ - {x^2}}}{2} + 2x - \dfrac{1}{2}\) là \(\left( {2;\dfrac{3}{2}} \right)\). Dựa vào đồ thị, để (*) có ba nghiệm phân biệt thì \(m \in \left\{ {\dfrac{1}{2};1;\dfrac{3}{2}} \right\}\). Tổng tất cả các giá trị của tham số \(m\) thỏa mãn là \(\dfrac{1}{2} + 1 + \dfrac{3}{2} = 3\).