Câu hỏi:
2 năm trước
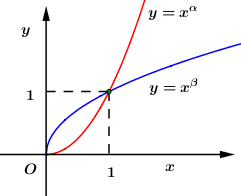
Cho \(\alpha ,\,\,\beta \) là các số thực. Đồ thị các hàm số \(y = {x^\alpha },\,\,y = {x^\beta }\) trên khoảng \(\left( {0; + \infty } \right)\) được cho hình vẽ bên. Khẳng định nào sau đây đúng?
Trả lời bởi giáo viên
Đáp án đúng: a
Dựa vào đồ thị hàm số ta thấy hàm số \(y = {x^\alpha }\) là hàm số đồng biến trên \(\left( {0; + \infty } \right) \Rightarrow \alpha > 1.\)
Hàm số \(y = {x^\beta }\) nghịch biến trên \(\left( {0; + \infty } \right) \Rightarrow 0 < \beta < 1.\)
\( \Rightarrow 0 < \beta < 1 < \alpha .\)
Hướng dẫn giải:
Dựa vào tính đơn điệu và tập xác định của hàm số lũy thừa:
+) Hàm số \({x^n}\) xác định \( \Leftrightarrow \left[ \begin{array}{l}x \in \mathbb{R}\,\,\,\,khi\,\,\,n \in {\mathbb{Z}^ + }\\x \in \mathbb{R}\backslash \left\{ 0 \right\}\,\,\,\,\,khi\,\,\,n \in {\mathbb{Z}^ - }\\x \in \left( {0; + \infty } \right)\,\,\,khi\,\,\,n \notin \mathbb{Z}\end{array} \right..\)
