Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có độ dài cạnh đáy \(AB = 6\), cạnh bên bằng \(\sqrt 5 \) (minh họa như hình vẽ). Gọi \(M\) là trung điểm của cạnh \(A'C'\).

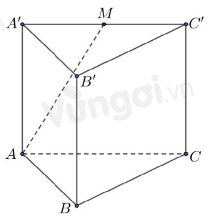
Khoảng cách từ \(B'\) đến mặt phẳng \(\left( {ABM} \right)\) bằng \(\dfrac{{3\sqrt a }}{{47}}\). Tính $a$.

Điền số nguyên hoặc phân số dạng a/b

Đáp án:

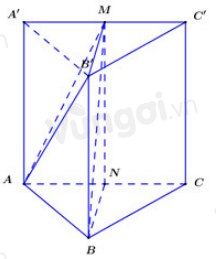
Gọi \(N\) là trung điểm \(AC\).

\( \Rightarrow \left( {BB'M} \right) \equiv \left( {BB'MN} \right)\).

Khi đó \(d\left( {A,\left( {BB'M} \right)} \right) = d\left( {A,\left( {BB'MN} \right)} \right)\).

Vì tam giác \(ABC\) đều nên \(AN \bot BN\).

Ta có \(\left\{ \begin{array}{l}AN \bot BN\\AN \bot MN\\BN,MN \subset \left( {BB'MN} \right)\end{array} \right.\)

\( \Rightarrow AN \bot \left( {BB'MN} \right)\).

\( \Rightarrow d\left( {A,\left( {BB'MN} \right)} \right) = AN = \dfrac{{AC}}{2} = \dfrac{6}{2} = 3\).

Ta lại có \(BN = \dfrac{{AB\sqrt 3 }}{2} = \dfrac{{6\sqrt 3 }}{2} = 3\sqrt 3 \) và \(MN = AA' = \sqrt 5 \).

\( \Rightarrow {S_{BB'MN}} = BN.MN = 3\sqrt 3 .\sqrt 5  = 3\sqrt {15} \)

\( \Rightarrow {S_{BB'M}} = \dfrac{{{S_{BB'MN}}}}{2} = \dfrac{{3\sqrt {15} }}{2}\).

\( \Rightarrow {V_{A.BB'M}} = \dfrac{1}{3}.d\left( {A,\left( {BB'M} \right)} \right).{S_{BB'M}} = \dfrac{1}{3}.3.\dfrac{{3\sqrt {15} }}{2} = \dfrac{{3\sqrt {15} }}{2} = {V_{B'.ABM}}\).

Tam giác \(AA'M\) vuông tại \(A'\): \(AM = \sqrt {A{{A'}^2} + A'{M^2}}  = \sqrt {5 + {3^2}}  = \sqrt {14} \).

Tam giác \(BB'M\) vuông tại \(B'\): \(BM = \sqrt {B{{B'}^2} + B'{M^2}}  = \sqrt {5 + {{\left( {3\sqrt 3 } \right)}^2}}  = 4\sqrt 2 \).

Áp dụng công thức Hê–rông, ta có \({S_{ABM}} = \sqrt {p\left( {p - AM} \right)\left( {p - AB} \right)\left( {p - BM} \right)}  = \dfrac{{3\sqrt {47} }}{2}\)

Ta có \({V_{B'.ABM}} = \dfrac{1}{3}.d\left( {B',\left( {ABM} \right)} \right).{S_{ABM}}\)

\( \Rightarrow d\left( {B',\left( {ABM} \right)} \right) = \dfrac{{3.{V_{B'.ABM}}}}{{{S_{ABM}}}} = \dfrac{{3.\dfrac{{3\sqrt {15} }}{2}}}{{\dfrac{{3\sqrt {47} }}{2}}} = \dfrac{{3\sqrt {705} }}{{47}}\).

Khoảng cách từ \(B'\) đến mặt phẳng \(\left( {ABM} \right)\) bằng \(\dfrac{{3\sqrt {705} }}{{47}}\).

Vậy $a=705$.