Câu hỏi:
2 năm trước
Đề thi THPT QG 2019 – mã đề 104
Cho lăng trụ \(ABC.A'B'C'\) có chiều cao bằng 4 và đáy là tam giác đều cạnh bằng 4. Gọi \(M,N\) và \(P\) lần lượt là tâm của các mặt bên \(ABB'A',ACC'A'\) và \(BCC'B'\). Thể tích của khối đa diện lồi có các đỉnh là các điểm \(A,B,C,M,N,P\) bằng
Trả lời bởi giáo viên
Đáp án đúng: c
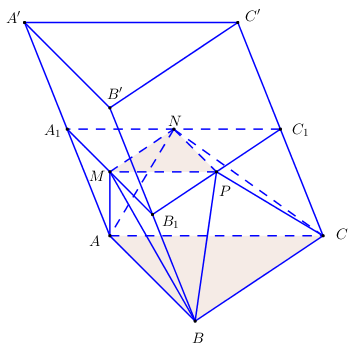
Gọi \(V\) là thể tích khối lăng trụ \(ABC.A'B'C'\).
Gọi \({A_1},\,\,{B_1},\,\,{C_1}\) lần lượt là trung điểm của \(AA',\,\,BB',\,\,CC'\). Khi đó ta có \(\left( {{A_1}{B_1}{C_1}} \right)//\left( {ABC} \right)//\left( {A'B'C'} \right)\)
Khi đó \({V_{ABC.MNP}} = {V_{ABC.{A_1}{B_1}{C_1}}} - {V_{A.{A_1}MN}} - {V_{B.{B_1}MP}} - {V_{C.{C_1}NP}}\).
Ta có \({V_{ABC.{A_1}{B_1}{C_1}}} = \dfrac{1}{2}{V_{ABC.A'B'C'}} = \dfrac{1}{2}V\).
\({V_{A.{A_1}MN}} = \dfrac{1}{3}d\left( {A;\left( {{A_1}{B_1}{C_1}} \right)} \right).{S_{{A_1}MN}}\)\( = \dfrac{1}{3}.\dfrac{1}{2}d\left( {\left( {ABC} \right);\left( {A'B'C'} \right)} \right).\dfrac{1}{4}{S_{ABC}} = \dfrac{1}{{24}}V\).
Chứng minh tương tự ta có \({V_{B.{B_1}MP}} = {V_{C.{C_1}NP}} = \dfrac{V}{{24}}\).
\( \Rightarrow {V_{ABCMNP}} = \dfrac{1}{2}V - 3.\dfrac{V}{{24}} = \dfrac{{3V}}{8}\).
Ta có \(V = 4.\dfrac{{{4^2}\sqrt 3 }}{4} = 16\sqrt 3 \)\( \Rightarrow {V_{ABCMNP}} = \dfrac{{3.16\sqrt 3 }}{8} = 6\sqrt 3 \).
Hướng dẫn giải:
+) Gọi \({A_1},\,\,{B_1},\,\,{C_1}\) lần lượt là trung điểm của \(AA',\,\,BB',\,\,CC'\).
+) Sử dụng phương pháp tổng, hiệu thể tích.
+) Biến đổi các thể tích theo thể tích của lăng trụ \(ABC.A'B'C'\)
Câu hỏi khác
- Bài tập thể tích khối chóp toán 12 có lời giải
- Bài tập thể tích lăng trụ, khối hộp toán 12 có lời giải
- Bài tập khối đa diện đều, phép vị tự toán 12 có lời giải
- Bài tập khái niệm về khối đa diện (sự bằng nhau của các khối đa diện) toán 12 có lời giải
- Bài tập khái niệm về khối đa diện toán 12 có lời giải
