Câu hỏi:
2 năm trước
Cho khối lăng trụ \(ABC.A'B'C'\). Gọi \(E,\,\,F\) lần lượt là trung điểm của \(AA',\,\,CC'\). Mặt phẳng \(\left( {BEF} \right)\) chia khối lăng trụ thành hai phần. Tỉ số thể tích của hai phần đó là:
Trả lời bởi giáo viên
Đáp án đúng: c
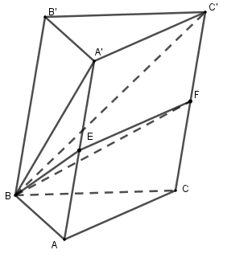
Ta có: \({V_{ABC.A'B'C'}} = d\left( {B;\left( {A'B'C'} \right)} \right).{S_{A'B'C'}} = V\)
\({V_{B.A'B'C'}} = \dfrac{1}{3}d\left( {B;\left( {A'B'C'} \right)} \right).{S_{A'B'C'}} = \dfrac{1}{3}V\)
Suy ra \({V_{B.AA'C'C}} = {V_{ABC.A'B'C'}} - {V_{B.A'B'C'}}\) \( = V - \dfrac{1}{3}V = \dfrac{2}{3}V\)
Lại có: \({S_{ACFE}} = \dfrac{1}{2}{S_{AA'C'C}}\) (do E, F lần lượt là trung điểm của AA’, CC’)
Suy ra \({V_{B.AEFC}} = \dfrac{1}{3}d\left( {B,\left( {AA'C'C} \right)} \right).{S_{ACFE}}\) \( = \dfrac{1}{3}d\left( {B,\left( {AA'C'C} \right)} \right).\dfrac{1}{2}{S_{AA'C'C}}\)
\( = \dfrac{1}{2}.\dfrac{1}{3}d\left( {B,\left( {AA'C'C} \right)} \right).{S_{AA'C'C}}\) \( = \dfrac{1}{2}{V_{B.AA'C'C}} = \dfrac{1}{2}.\dfrac{2}{3}V = \dfrac{1}{3}V\)
Suy ra \({V_{BEFA'B'C'}} = {V_{ABC.A'B'C'}} - {V_{B.ACFE}}\) \( = V - \dfrac{1}{3}V = \dfrac{2}{3}V\)
Vậy tỉ số thể tích giữa hai phần là: \({V_{B.ACFE}}:{V_{BEFA'B'C'}} = \dfrac{1}{3}V:\dfrac{2}{3}V = 1:2\)
Hướng dẫn giải:
Sử dụng phân chia thể tích.
Sử dụng công thức tính thể tích hình chóp \(V = \dfrac{1}{3}h.S\) , thể tích lăng trụ \(V = h.S\)
Câu hỏi khác
- Bài tập thể tích khối chóp toán 12 có lời giải
- Bài tập thể tích lăng trụ, khối hộp toán 12 có lời giải
- Bài tập khối đa diện đều, phép vị tự toán 12 có lời giải
- Bài tập khái niệm về khối đa diện (sự bằng nhau của các khối đa diện) toán 12 có lời giải
- Bài tập khái niệm về khối đa diện toán 12 có lời giải
