Câu hỏi:
1 năm trước
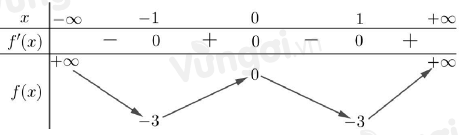
Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:
Phương trình \(f\left( {{x^2} - 1} \right) + 2 = 0\) có bao nhiêu nghiệm thực?
Điền số nguyên hoặc phân số dạng a/b
Đáp án:
Trả lời bởi giáo viên
Đáp án:
Đáp án:
Đặt \(t = {x^2} - 1\,\,\left( {t \ge - 1} \right)\).
Phương trình đã cho trở thành: \(f\left( t \right) + 2 = 0\).
\( \Leftrightarrow f\left( t \right) = - 2\), với \(t \ge - 1\) (*).
Dựa vào bảng biến thiên, ta thấy đường thẳng \(y = - 2\) cắt đồ thị hàm số \(y = f\left( t \right)\) tại 4 điểm phân biệt. Trong đó, có 3 điểm phân biệt có hoành độ lớn hơn hoặc bằng \( - 1\).
Suy ra phương trình (*) có 3 nghiệm thực \(t\).
Khi đó ứng với mỗi nghiệm thực \(t\) thì có 2 nghiệm thực \(x\).
Vậy phương trình đã cho có tổng cộng 6 nghiệm thực phân biệt.
Hướng dẫn giải:
Bước 1: Đổi biến \(t = {x^2} - 1\,\,\left( {t \ge - 1} \right)\). Biến đổi phương trình \(f\left( {{x^2} - 1} \right) + 2 = 0\) theo ẩn \(t\).
Bước 2: Dựa vào bảng biến thiên, ta biện luận số nghiệm của phương trình theo ẩn \(t\). Từ đó suy ra số nghiệm của phương trình theo ẩn \(x\) ban đầu.
Câu hỏi khác
- Bài tập sự đồng biến, nghịch biến của hàm số toán 12 có lời giải
- Bài tập cực trị của hàm số toán 12 có lời giải
- Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số toán 12 có lời giải
- Bài tập cực trị có tham số đối với các hàm số cơ bản môn Toán lớp 12
- Bài tập đồ thị của hàm số và phép tịnh tiến hệ tọa độ toán 12 có lời giải
