Câu hỏi:
2 năm trước
Phương trình \({x^3} - 3{x^2} + m = 0\) có ba nghiệm phân biệt khi và chỉ khi m thuộc khoảng
Trả lời bởi giáo viên
Đáp án đúng: b
Bước 1:
Ta có: \({x^3} - 3{x^2} = - m\)
Bước 2:
Đặt \(y = f\left( x \right) = {x^3} - 3{x^2}\) , ta có: \(f'\left( x \right) = 3{x^2} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\)
BBT của hàm số \(f\left( x \right) = {x^3} - 3{x^2}\)
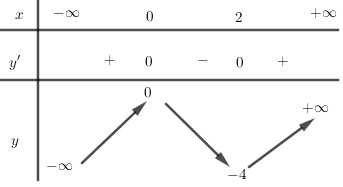
Bước 3:
Đường thẳng \(y = - m\) cắt đồ thị hàm số \(f\left( x \right) = {x^3} - 3{x^2}\) tại ba điểm phân biệt khi \( - 4 < - m < 0 \Leftrightarrow 0 < m < 4\)
Hướng dẫn giải:
Bước 1: Tách m về 1 vế đưa phương trình về dạng \(f\left( x \right) = m\)
Bước 2: Lập bảng biến thiên của hàm số \(y = f\left( x \right)\)
Bước 3: Phương trình trên có 3 nghiệm phân biệt khi đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại ba điểm phân biệt.
Câu hỏi khác
- Bài tập sự đồng biến, nghịch biến của hàm số toán 12 có lời giải
- Bài tập cực trị của hàm số toán 12 có lời giải
- Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số toán 12 có lời giải
- Bài tập cực trị có tham số đối với các hàm số cơ bản môn Toán lớp 12
- Bài tập đồ thị của hàm số và phép tịnh tiến hệ tọa độ toán 12 có lời giải
