Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên:
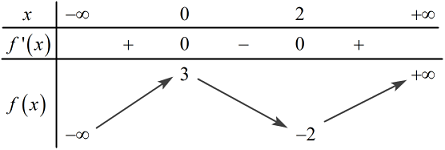
Số nghiệm của phương trình \(2f\left( x \right) - 3 = 0\) là:
Trả lời bởi giáo viên
Số nghiệm của phương trình \(2f\left( x \right) - 3 = 0 \Leftrightarrow f\left( x \right) = \frac{3}{2}\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = \frac{3}{2}\)
Ta có BBT:
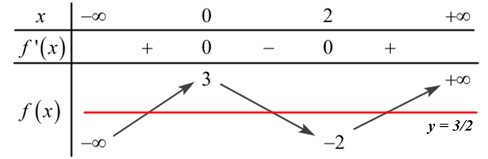
Dựa vào BBT ta thấy đường thẳng \(y = \frac{3}{2}\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 3 điểm phân biệt
\( \Rightarrow \) Phương trình \(2f\left( x \right) - 3 = 0\) có 3 nghiệm phân biệt.
Hướng dẫn giải:
Số nghiệm của phương trình \(2f\left( x \right) - 3 = 0 \Leftrightarrow f\left( x \right) = \frac{3}{2}\) là số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = \frac{3}{2}\)
Dựa vào BBT để biện luận số nghiệm của phương trình.

