Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau:

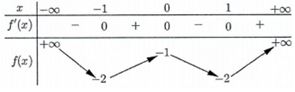
Số nghiệm thuộc đoạn \(\left[ { - \pi ;2\pi } \right]\) của phương trình \(2f\left( {\sin x} \right) + 3 = 0\) là:

Phương trình \(2f\left( {\sin x} \right) + 3 = 0 \Leftrightarrow f\left( {\sin x} \right) =  - \dfrac{3}{2}\,\,\,\,\left( * \right)\) có nghiệm trên \(\left[ { - \pi ;\,\,2\pi } \right]\) \( \Leftrightarrow \) đường thẳng \(y =  - \dfrac{3}{2}\) cắt đồ thị hàm số \(y = f\left( {\sin x} \right)\) tại các điểm trên \(\left[ { - \pi ;\,\,2\pi } \right].\)

Đặt \(\sin x = t \Rightarrow x \in \left[ { - \pi ;\,\,2\pi } \right] \Rightarrow t \in \left[ { - 1;\,\,1} \right].\)

Ta có BBT:

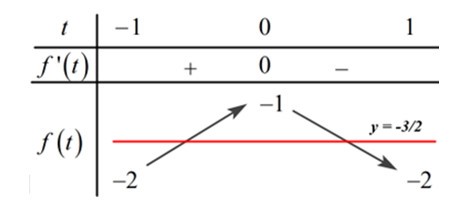
Dựa vào BBT ta có: đường thẳng \(y =  - \frac{3}{2}\) cắt đồ thị hàm số \(y = f\left( t \right)\) tại hai điểm phân biệt.

Ta có \(\left( * \right) \Leftrightarrow \left[ \begin{array}{l}\sin x = {t_1} \in \left( {0;1} \right)\\\sin x = {t_2} \in \left( { - 1;0} \right)\end{array} \right.\).

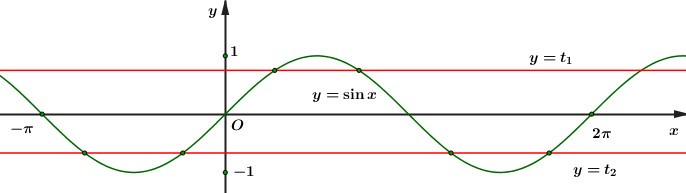
Dựa vào đồ thị hàm số ta thấy:

+) Đường thẳng \(y = {t_1}\) cắt đồ thị hàm số \(y = \sin x\) tại hai điểm phân biệt trong \(\left[ { - \pi ;\,\,2\pi } \right].\)

+) Đường thẳng \(y = {t_2}\) cắt đồ thị hàm số \(y = \sin x\) tại bốn điểm phân biệt trong \(\left[ { - \pi ;\,\,2\pi } \right].\)

Như vậy đường thẳng \(y =  - \frac{3}{2}\) cắt đồ thị hàm số \(y = f\left( {\sin x} \right)\) tại 6 điểm phân biệt trên \(\left[ { - \pi ;\,\,2\pi } \right].\)

Vậy phương trình đã cho có 6 nghiệm phân biệt.