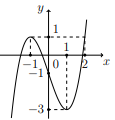
Cho hàm số \(f\left( x \right)\) có đồ thị trong hình bên. Phương trình \(f\left[ {f\left( {\cos x} \right) - 1} \right] = 0\) có bao nhiêu nghiệm thuộc đoạn \(\left[ {0;2\pi } \right]?\)

Đặt \(t = f\left( {\cos x} \right) - 1\), phương trình trở thành \(f\left( t \right) = 0\).

Dựa vào đồ thị hàm số ta thấy \(f\left( t \right) = 0 \Leftrightarrow \left[ \begin{array}{l}t = a \in \left( { - 2; - 1} \right)\\t = b \in \left( { - 1;0} \right)\\t = c \in \left( {1;2} \right)\end{array} \right.\)

Khi đó ta có: \(\left[ \begin{array}{l}f\left( {\cos x} \right) - 1 = a \in \left( { - \infty ; - 1} \right)\\f\left( {\cos x} \right) - 1 = b \in \left( { - 1;0} \right)\\f\left( {\cos x} \right) - 1 = c \in \left( {1;2} \right)\end{array} \right. \Rightarrow \left[ \begin{array}{l}f\left( {\cos x} \right) = a + 1 \in \left( { - 1;0} \right)\,\,\,\left( 1 \right)\\f\left( {\cos x} \right) = b + 1 \in \left( {0;1} \right)\,\,\,\,\,\,\,\left( 2 \right)\\f\left( {\cos x} \right) = c + 1 \in \left( {2;3} \right)\,\,\,\,\,\,\,\left( 3 \right)\end{array} \right.\)

Tiếp tục dựa vào đồ thị hàm số ta có:

\(\left( 1 \right) \Leftrightarrow \left[ \begin{array}{l}\cos x = {a_1} <  - 1\,\,\,\,\,\,\,\,\,\,\,\,\left( {1.1} \right)\\\cos x = {a_2} \in \left( { - 1;0} \right)\,\,\,\,\left( {1.2} \right)\\\cos x = {a_3} > 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {1.3} \right)\end{array} \right.\)

Các phương trình (1.1), (1.3) vô nghiệm do \( - 1 \le \cos x \le 1\), phương trình (1.2) có 2 nghiệm phân biệt thuộc \(\left[ {0;2\pi } \right]\).

\(\left( 2 \right) \Leftrightarrow \left[ \begin{array}{l}\cos x = {b_1} <  - 1\,\,\,\,\,\,\,\,\,\,\,\left( {2.1} \right)\\\cos x = {b_2} \in \left( { - 1;0} \right)\,\,\,\left( {2.2} \right)\\\cos x = {b_3} > 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {2.3} \right)\end{array} \right.\)

Các phương trình (1.1), (1.3) vô nghiệm do \( - 1 \le \cos x \le 1\), phương trình (1.2) có 2 nghiệm phân biệt thuộc \(\left[ {0;2\pi } \right]\).

\(\left( 3 \right) \Leftrightarrow \cos x = {c_1} > 1 \Rightarrow \) Phương trình vô nghiệm.

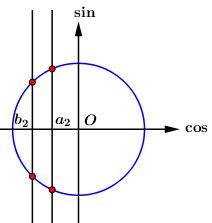
Vậy phương trình ban đầu có 4 nghiệm phân biệt thuộc \(\left[ {0;2\pi } \right]\).