Cho hàm số \(y = f\left( x \right)\) có đồ thị trong hình sau:

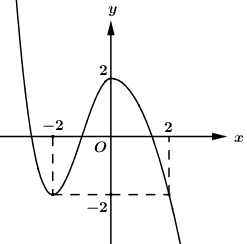
Số nghiệm của phương trình \(f\left( {{x^3} - 3x} \right) + 1 = 0\) trong khoảng \(\left( {0;2} \right)\) là: 

Đặt \(t = {x^3} - 3x\) ta có \(t' = 3{x^2} - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 \in \left( {0;2} \right)\\x =  - 1 \notin \left( {0;2} \right)\end{array} \right.\).

Ta có BBT:

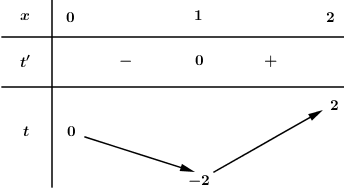
Suy ra \(x \in \left( {0;2} \right)\) thì \(t \in \left[ { - 2;2} \right)\).

Khi đó phương trình trở thành \(f\left( t \right) + 1 = 0 \Leftrightarrow f\left( t \right) =  - 1\).

Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y = f\left( t \right)\) và đường thẳng \(y =  - 1\).

Dựa vào đồ thị hàm số ta thấy đường thẳng \(y =  - 1\) cắt đồ thị hàm số \(y = f\left( t \right)\) tại 3 điểm phân biệt, do đó phương trình \(f\left( t \right) =  - 1\) có 3 nghiệm phân biệt \(\left[ \begin{array}{l}t = a \in \left( { - \infty ; - 2} \right)\,\,\left( {ktm} \right)\\t = b \in \left( { - 2;0} \right)\\t = c \in \left( {0;2} \right)\end{array} \right.\).

Dựa vào BBT hàm số \(t = {x^3} - 3x\) ta có:

+ Phương trình \(t = b \in \left( { - 2;0} \right)\) có 2 nghiệm phân biệt.

+ Phương trình \(t = c \in \left( {0;2} \right)\) có 1 nghiệm duy nhất.

Vậy phương trình đã cho có tất cả 3 nghiệm.