Có bao nhiêu giá trị nguyên dương của m để phương trình \(\left| {{x^3} - 3{x^2} + 2} \right| = m\) có đúng 6 nghiệm thực phân biệt.

Số nghiệm của phương trình \(\left| {{x^3} - 3{x^2} + 2} \right| = m\) là số giao điểm của đồ thị hàm số \(y = \left| {{x^3} - 3{x^2} + 2} \right|\) và đường thẳng \(y = m\) song song với trục hoành.

Xét hàm số \(y = {x^3} - 3{x^2} + 2\) ta có:

+ TXĐ: \(D = \mathbb{R}\).

+ \(y' = 3{x^2} - 6x\), \(y' = 0 \Leftrightarrow 3x\left( {x - 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\).

+ \(\left\{ \begin{array}{l}x = 0 \Rightarrow y = 2\\x = 2 \Rightarrow y =  - 2\end{array} \right.\)

Ta vẽ được đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\) như sau:

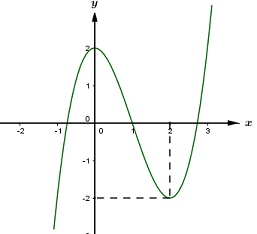
Từ đó ta vẽ được đồ thị hàm số \(y = \left| {{x^3} - 3{x^2} + 2} \right|\) như sau:

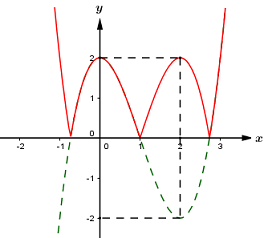
(Đường màu đỏ)

Dựa vào đồ thị hàm số ta thấy phương trình \(\left| {{x^3} - 3{x^2} + 2} \right| = m\) có 6 nghiệm phân biệt khi và chỉ khi \(0 < m < 2\).

Mà m nguyên dương \( \Rightarrow m = 1\).

Vậy có 1 giá trị của m thỏa mãn yêu cầu bài toán.