Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(|\sin x - \cos x| + \) \(4\sin 2x = m\) có nghiệm thực?

Đặt \(t = |\sin x - \cos x|\)\( = \sqrt 2 \left| {\sin \left( {x - \dfrac{\pi }{4}} \right)} \right| \in [0;\sqrt 2 ]\)

\( \Rightarrow {t^2} = 1 - \sin 2x \Leftrightarrow \sin 2x = 1 - {t^2}.\)

Phương trình đã cho trở thành \(t + 4\left( {1 - {t^2}} \right) = m\)\( \Leftrightarrow  - 4{t^2} + t + 4 = m(*)\)

Phương trình đã cho có nghiệm thực \( \Leftrightarrow \) Phương trình \((*)\) có nghiệm thực trên \([0;\sqrt 2 ]\).

Xét hàm số \(f(t) =  - 4{t^2} + t + 4\) trên \([0;\sqrt 2 ]\).

Ta có \({f^\prime }(t) =  - 8t + 1\).

\( \Rightarrow {f^\prime }(t) = 0 \Leftrightarrow  - 8t + 1 = 0\)\( \Leftrightarrow t = \dfrac{1}{8}\)

Ta có bảng biến thiên

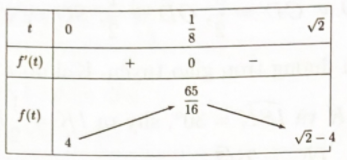
Dựa vào bảng biến thiên ta có yêu cầu bài toán \( \Leftrightarrow \sqrt 2  - 4 \le m \le \dfrac{{65}}{{16}}\).

Do \(m \in \mathbb{Z} \Rightarrow m \in \{  - 2; - 1;0;1;2;3;4\} \). Vậy có 7 giá trị nguyên của \(m\) thỏa mãn yêu cầu bài toán.