Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
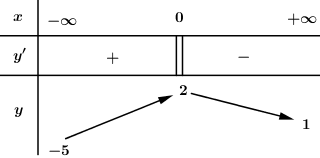
Có bao nhiêu giá trị nguyên của \(m\) để phương trình \(f\left( x \right) = m\) có nghiệm duy nhất?
Trả lời bởi giáo viên
Phương trình \(f\left( x \right) = m\) là có nghiệm duy nhất \( \Leftrightarrow \) đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 1 điểm duy nhất.
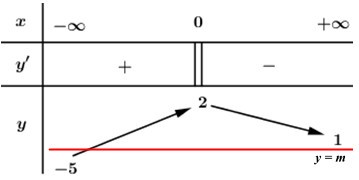
Dựa vào BBT ta thấy, đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 1 điểm duy nhất \( \Leftrightarrow \left[ \begin{array}{l} - 5 < m \le 1\\m = 2\end{array} \right.\)
Lại có: \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 4; - 3; - 2; - 1;\,\,0;\,\,1;\,\,2} \right\}\)
Vậy có 7 giá trị nguyên của m thỏa mãn bài toán.
Hướng dẫn giải:
Phương trình \(f\left( x \right) = m\) là có nghiệm duy nhất \( \Leftrightarrow \) đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 1 điểm duy nhất.
Dựa vào BBT để xác định \(m.\)

