Gọi \(S\) là tập các số nguyên \(m \in [ - 5;5]\) để phương trình \(2x - 2\sqrt {x - \sqrt {{x^2} - 4} } \)\( + \sqrt {x + \sqrt {{x^2} - 4} } \)\( = 2m + 2\sqrt {{x^2} - 4} \) có nghiệm. Số tập con của tập \(S\) là

Bước 1: Tìm điều kiện xác định.

Điều kiện xác định \(\left\{ {\begin{array}{*{20}{l}}{{x^2} - 4 \ge 0}\\{x - \sqrt {{x^2} - 4}  \ge 0 \Leftrightarrow x \ge 2}\\{x + \sqrt {{x^2} - 4}  \ge 0}\end{array}} \right.\)

Bước 2: Đặt \(t = \sqrt {x - \sqrt {{x^2} - 4} } (0 < t \le \sqrt 2 )\)

Nhận xét: \(\sqrt {x - \sqrt {{x^2} - 4} }  \cdot \sqrt {x + \sqrt {{x^2} - 4} }  = 2\).

Đặt \(t = \sqrt {x - \sqrt {{x^2} - 4} } (0 < t \le \sqrt 2 )\). Phương trình trên trở thành:

\(2{t^2} - 2t + \dfrac{2}{t} = 2m\)\( \Leftrightarrow {t^2} - t + \dfrac{1}{t} = m\)

Bước 3: Xét hàm số \(f(t) = {t^2} - t + \dfrac{1}{t}\), lập bảng biến thiên

Xét hàm số \(f(t) = {t^2} - t + \dfrac{1}{t}\), với \(0 < t \le \sqrt 2 \).

Do đó \({f^\prime }(t) = 2t - 1 - \dfrac{1}{{{t^2}}},\)

\({f^\prime }(t) = 0 \Leftrightarrow t = 1\).

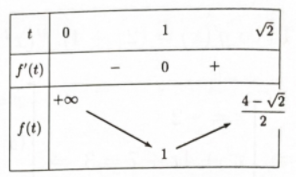
Bước 4: Tìm số tập con của tập hợp \(S\)

Dựa vào bảng biến thiên, để phương trình có nghiệm thì \(m \ge 1\).

Vì \(m \in \mathbb{Z}\) và \(m \in [ - 5;5]\) nên ta có \(S = \{ 1;2;3;4;5\} \).

Vậy số tập con của tập hợp \(S\) là \({2^5} = 32\).