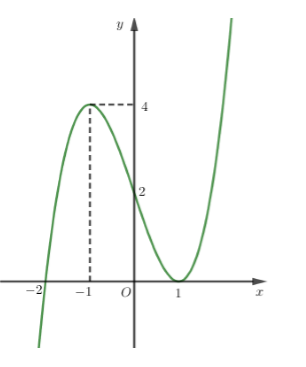
Cho hàm số $y = f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$ và hàm số $y = f'\left( x \right)$ có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng ?

Có bao nhiêu số nguyên \(m \in \left( { - 7;7} \right)\) để đồ thị hàm số \(y = \left| {{x^4} - 3m{x^2} - 4} \right|\) có đúng ba điểm cực trị \(A,B,C\) và diện tích tam giác \(ABC\) lớn hơn 4.

Cho hàm số \(y = {x^3} - 6mx + 4\) có đồ thị \(\left( {{C_m}} \right)\). Gọi \({m_0}\) là giá trị của \(m\) để đường thẳng đi qua điểm cực đại, điểm cực tiểu của \(\left( {{C_m}} \right)\) cắt đường tròn tâm \(I\left( {1;0} \right)\), bán kính \(\sqrt 2 \) tại hai điểm phân biệt \(A,B\) sao cho tam giác \(IAB\) có diện tích lớn nhất. Chọn khẳng định đúng?

Tìm tất cả các giá trị của tham số \(m\) để hàm số \(y = \dfrac{1}{3}{x^3} - \left( {2m - 1} \right){x^2} + \left( {{m^2} - m + 7} \right)x + m - 5\) có hai điểm cực trị là độ dài hai cạnh góc vuông của một tam giác vuông có cạnh huyền bằng \(\sqrt {74} \).

Tìm tất cả các giá trị thực của tham số m để hàm số $y = {x^3} - 3{x^2} + (m + 1)x + 2$ có hai điểm cực trị.

Tìm tất cả các giá trị thực của $m$ để hàm số $y = {x^4} + 2\left( {{m^2} - 9} \right){x^2} + 5m + 2$ có cực đại, cực tiểu

Hàm số $y = m{x^4} + \left( {m + 3} \right){x^2} + 2m - 1$ chỉ có cực đại mà không có cực tiểu khi

Hàm số  $y = {x^3} + 2a{x^2} + 4bx - 2018,{\mkern 1mu} {\mkern 1mu} (a,{\mkern 1mu} b \in R)$ đạt cực trị tại  $x =  - 1$ . Khi đó hiệu  $a - b$ là: