Cho hàm số \(y = {x^3} - 6mx + 4\) có đồ thị \(\left( {{C_m}} \right)\). Gọi \({m_0}\) là giá trị của \(m\) để đường thẳng đi qua điểm cực đại, điểm cực tiểu của \(\left( {{C_m}} \right)\) cắt đường tròn tâm \(I\left( {1;0} \right)\), bán kính \(\sqrt 2 \) tại hai điểm phân biệt \(A,B\) sao cho tam giác \(IAB\) có diện tích lớn nhất. Chọn khẳng định đúng?

Ta có: \(y' = 3{x^2} - 6m \Rightarrow y = y'.\left( {\dfrac{1}{3}x} \right) - 4mx + 4\).

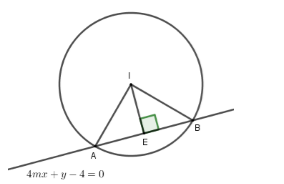
Do đó phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là \(y =  - 4mx + 4 \Leftrightarrow 4mx + y - 4 = 0\).

Diện tích tam giác \(IAB\) là \({S_{IAB}} = \dfrac{1}{2}IA.IB.\sin \widehat {AIB} = \dfrac{1}{2}.\sqrt 2 .\sqrt 2 .\sin \widehat {AIB} = \sin \widehat {AIB} \le 1\)

\( \Rightarrow {S_{IAB}}\) đạt GTLN khi \(\sin \angle AIB = 1 \Leftrightarrow IA \bot IB\) hay tam giác \(IAB\) vuông cân tại \(I\) và \(IA = IB = \sqrt 2 \)\( \Rightarrow AB = 2 \Rightarrow d\left( {I,AB} \right) = \dfrac{1}{2}AB = 1.\)

\(\begin{array}{l} \Rightarrow \dfrac{{\left| {4m.1 + 0 - 4} \right|}}{{\sqrt {{{\left( {4m} \right)}^2} + {1^2}} }} = 1 \Leftrightarrow \left| {4m - 4} \right| = \sqrt {{{\left( {4m} \right)}^2} + {1^2}} \\ \Leftrightarrow 16{m^2} - 32m + 16 = 16{m^2} + 1 \Leftrightarrow m = \dfrac{{15}}{{32}} \in \left( {0;1} \right)\end{array}\)