Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau
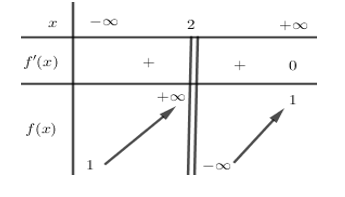
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Từ BBT ta thấy $f'\left( x \right) > 0,\forall x \in \left( {2; + \infty {\rm{\;}}} \right)$nên hàm số đồng biến trên khoảng $\left( {2; + \infty {\rm{\;}}} \right)$.
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như hình vẽ bên. Mệnh đề nào sau đây là sai ?
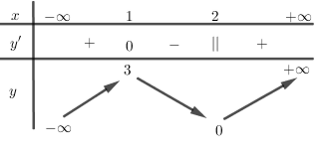
Dựa vào BBT ta thấy :
Hàm số đồng biến trên các khoảng $\left( { - \infty ;1} \right),\left( {2; + \infty } \right)$ và nghịch biến trên \(\left( {1;2} \right)\)
Cho hàm số $y = f\left( x \right)$ có đạo hàm trên khoảng $\left( {a;b} \right).$ Mệnh đề nào sau đây sai ?
Nếu hàm số $y = f\left( x \right)$ đồng biến trên $\left( {a;b} \right)$ thì $f'\left( x \right) \ge 0$ với mọi $x \in \left( {a;b} \right).$
Chẳng hạn hàm số \(y = f\left( x \right) = {x^3}\) đồng biến trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = 3{x^2} \ge 0,\forall x \in \mathbb{R}\).
Đề thi THPT QG 2019 – mã đề 104
Cho hàm số \(f\left( x \right)\) , bảng xét dấu của \(f'\left( x \right)\) như sau:
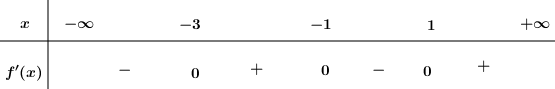
Hàm số \(y = f\left( {5 - 2x} \right)\) đồng biến trên khoảng nào dưới đây?
Ta có \(y' = \left[ {f\left( {5 - 2x} \right)} \right]' = - 2f'\left( {5 - 2x} \right)\).
Xét \(y' > 0 \Leftrightarrow - 2f'\left( {5 - 2x} \right) > 0\) \( \Leftrightarrow f'\left( {5 - 2x} \right) < 0\)
\( \Leftrightarrow \left[ \begin{array}{l}5 - 2x < - 3\\ - 1 < 5 - 2x < 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x > 4\\2 < x < 3\end{array} \right.\)
=> Hàm số đồng biến trên \(\left( {2;3} \right)\) và \(\left( {4; + \infty } \right)\).
Cho hàm số \(y = f\left( x \right)\) xác định và có đạo hàm trên \(\left( {a;b} \right)\). Chọn kết luận đúng:
Đáp án A: Nếu \(f'\left( x \right) \le 0,\forall x\left( {a;b} \right)\) thì \(f\left( x \right)\) chưa chắc đã nghịch biến trên \(\left( {a;b} \right)\), chẳng hạn hàm số \(y = f\left( x \right) = 2\) có \(f'\left( x \right) = 0 \le 0,\forall x\) nhưng đây là hàm hằng nên không nghịch biến, do đó A sai.
Đáp án B: Nếu \(f'\left( x \right) < 0,\forall x\left( {a;b} \right)\) thì \(f\left( x \right)\) nghịch biến trên \(\left( {a;b} \right)\) đúng.
Đáp án C: Nếu \(f'\left( x \right) = 0,\forall x\left( {a;b} \right)\) thì \(f\left( x \right)\) không đổi trên \(\left( {a;b} \right)\), chưa chắc nó đã có giá trị bằng \(0\) nên C sai.
Đáp án D: Nếu \(f'\left( x \right) \le 0,\forall x\left( {a;b} \right)\) thì \(f\left( x \right)\) không đổi trên \(\left( {a;b} \right)\) sai.
Cho hàm số $y = f\left( x \right)$ có đạo hàm trên khoảng $\left( {a;b} \right).$ Mệnh đề nào sau đây sai ?
Nếu hàm số $y = f\left( x \right)$ đồng biến trên $\left( {a;b} \right)$ thì $f'\left( x \right) \ge 0$ với mọi $x \in \left( {a;b} \right).$
Chẳng hạn hàm số \(y = f\left( x \right) = {x^3}\) đồng biến trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = 3{x^2} \ge 0,\forall x \in \mathbb{R}\).
Cho hàm số \(y = f\left( x \right)\) xác định và có đạo hàm \(f'\left( x \right) = \sqrt 5 {x^2}\) trên \(\mathbb{R}\). Chọn kết luận đúng:
Ta có: \(f'\left( x \right) = \sqrt 5 {x^2} \ge 0,\forall x \in \mathbb{R}\) và \(f'\left( x \right) = 0 \Leftrightarrow x = 0\) nên hàm số đồng biến trên \(\mathbb{R}\).
Cho hàm số \(y = f\left( x \right)\) xác định và có đạo hàm \(f'\left( x \right) = \left( {1 - \sqrt 2 } \right){x^2}\) trên \(\mathbb{R}\). Chọn kết luận đúng:
Ta có: \(f'\left( x \right) = \left( {1 - \sqrt 2 } \right){x^2} \le 0,\forall x \in \mathbb{R}\) và \(f'\left( x \right) = 0 \Leftrightarrow x = 0\) nên hàm số nghịch biến trên \(\mathbb{R}\).
Cho hàm số \(y = f\left( x \right)\) xác định và có đạo hàm \(f'\left( x \right) = - \left( {\sqrt 5 - 2} \right){x^2}\) trên \(\mathbb{R}\). Chọn kết luận đúng:
Ta có: \(f'\left( x \right) = - \left( {\sqrt 5 - 2} \right){x^2} \le 0,\forall x \in \mathbb{R}\) và \(f'\left( x \right) = 0 \Leftrightarrow x = 0\) nên hàm số nghịch biến trên \(\mathbb{R}\).
Hình bên là đồ thị hàm số \(y = f'\left( x \right)\) Hỏi hàm số \(y = f\left( x \right)\) nghịch biến trên khoảng nào dưới đây?
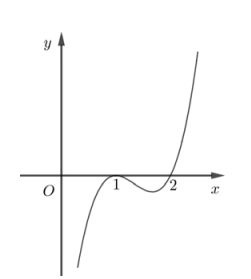
Ta thấy: $f'\left( x \right)$ mang dấu âm trong khoảng $\left( { - \infty ;2} \right)$
$ \Rightarrow $ Hàm số \(y=f(x)\) nghịch biến trên $\left( { - \infty ;2} \right)$
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = - {x^2} + 4\). Chọn khẳng định đúng:
Ta có: \(f'\left( x \right) = - {x^2} + 4 > 0 \Leftrightarrow - 2 < x < 2\) và \(f'\left( x \right) = - {x^2} + 4 < 0 \Leftrightarrow \left[ \begin{array}{l}x > 2\\x < - 2\end{array} \right.\)
Do đó hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( {2; + \infty } \right)\); đồng biến trên khoảng \(\left( { - 2;2} \right)\).
Trong các hàm số sau, hàm số nào nghịch biến trên $\left( {-\infty ; + \infty } \right)$?
Hàm số $y = {\rm{\;}} - {x^3} + {x^2} - 2x + 1$ có đạo hàm \(y' = - 3{x^2} + 2x - 2,\) \(\Delta ' = - 5 < 0,a = - 3 < 0\) nên \(y' < 0,\forall x \in \mathbb{R}\)
Vậy hàm số nghịch biến trên $\mathbb{R}$
Trong các hàm số sau, hàm số nào đồng biến trên $R?$
Nhận thấy $y = {x^3} + 3x + 2 \Rightarrow y' = 3{x^2} + 3 > 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \forall x \in R$ nên hàm số $y = {x^3} + 3x + 2$ đồng biến trên $R.$
Hàm số nào sau đây nghịch biến trên từng khoảng xác định?
Đáp án A ta có $y = 2x - \sin {\mkern 1mu} x \Rightarrow y' = 2 - \cos x > 0,{\mkern 1mu} {\mkern 1mu} \forall x$
$\Rightarrow $ Hàm số đồng biến trên R.
Đáp án B ta có $y' = {\rm{\;}} - 3{x^2} + 6x < 0 \Leftrightarrow x \in \left( { - \infty ;0} \right) \cup \left( {2; + \infty } \right)$
$\Rightarrow $ Hàm số không nghịch biến trên R.
Đáp án C ta có $y' = \dfrac{{ - 1}}{{{{\left( {x - 2} \right)}^2}}} < 0 $
$\Rightarrow $ Hàm số nghịch biến trên $\left( { - \infty ;2} \right)$ và $\left( {2; + \infty } \right) $
$\Rightarrow $ Hàm số nghịch biến trên từng khoảng xác định.
Đáp án D ta có $y' = 4{x^3} - 2x < 0$
\( \Leftrightarrow 2x\left( {2{x^2} - 1} \right) < 0 \Leftrightarrow \left[ \begin{array}{l}x < - \frac{1}{{\sqrt 2 }}\\0 < x < \frac{1}{{\sqrt 2 }}\end{array} \right.\)
\( \Rightarrow \) Hàm số nghịch biến trên các khoảng \(\left( { - \infty ; - \frac{1}{{\sqrt 2 }}} \right)\) và \(\left( {0;\frac{1}{{\sqrt 2 }}} \right)\) chứ không nghịch biến trên \(\mathbb{R}\).
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\left( { - \infty ; + \infty } \right),\) có bảng biến thiên như hình sau. Mệnh đề nào sau đây đúng?
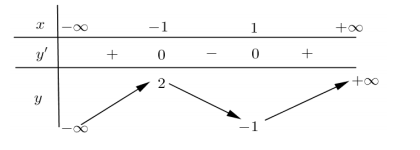
Dựa vào bảng biến thiên ta thấy
Hàm số đồng biến trên $\left( {1; + \infty } \right)$
Hàm số đồng biến trên $\left( { - \infty ; - 1} \right)$ do đó cũng đồng biến trên $\left( { - \infty ; - 2} \right)$
Trên các khoảng $\left( { - \infty ;1} \right)$ và $\left( { - 1; + \infty } \right)$ hàm số không đơn điệu (đồng biến hay nghịch biến)
Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như hình vẽ dưới đây. Khẳng định nào sau đây là sai?
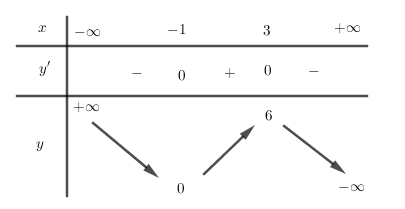
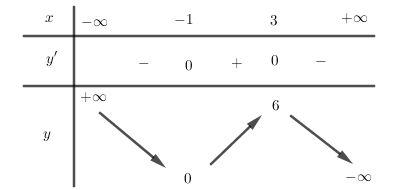
Trong khoảng $\left( {0;6} \right)$ ta thấy hàm số đồng biến trên khoảng $\left( {0;3} \right)$ và nghịch biến trên khoảng $\left( {3;6} \right)$ nên đáp án B sai.
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:
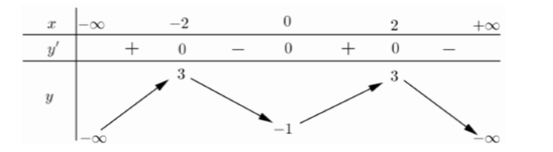
Hàm số $y = f\left( x \right)$ nghịch biến trên khoảng nào dưới đây?
Quan sát bảng biến thiên ta thấy hàm số nghịch biến trên các khoảng $\left( { - 2;0} \right)$ và $\left( {2; + \infty {\rm{\;}}} \right)$
Mà khoảng \(\left( { - 2; - 1} \right)\) nằm trong khoảng $\left( { - 2;0} \right)$ nên hàm số đã cho cũng nghịch biến trên \(\left( { - 2; - 1} \right)\)
Hàm số \(y = 2{x^4} + 1\) đồng biến trên khoảng nào?
Ta có $y' = 8{x^3} = 0 \Leftrightarrow x = 0;y' > 0 \Leftrightarrow x > 0$
Vậy hàm số đã cho đồng biến trên $\left( {0; + \infty } \right)$
Cho hàm số $y = {x^4} - 2{x^2} + 15$. Hàm số đồng biến trên khoảng nào dưới đây?
Đạo hàm: $y' = 4{x^3} - 4x $.
Hàm số đồng biến khi và chỉ khi:
$y' = 4{x^3} - 4x > 0$$ \Leftrightarrow 4x\left( {{x^2} - 1} \right) > 0 \Leftrightarrow \left[ \begin{array}{l}x > 1\\ - 1 < x < 0\end{array} \right.$ $ \Rightarrow x \in \left( { - 1;0} \right) \cup \left( {1; + \infty } \right)$
Do đó hàm số đồng biến trên các khoảng $\left( { - 1;0} \right)$ và $\left( {1; + \infty } \right)$
Hàm số $y = - {\mkern 1mu} {x^4} + 2{x^3} - 2x - 1$ nghịch biến trên khoảng nào sau đây ?
Ta có \(y' = - {\mkern 1mu} 4{x^3} + 6{x^2} - 2;{\mkern 1mu} {\mkern 1mu} \forall x \in \mathbb{R}.\)
Khi đó \(y' = 0 \Leftrightarrow - 4{x^3} + 6{x^2} - 2 = 0\)\( \Leftrightarrow - 2{\left( {x - 1} \right)^2}\left( {2x + 1} \right) =0\Leftrightarrow \left[ \begin{array}{l}x = - {\mkern 1mu} \dfrac{1}{2}\\x = 1\end{array} \right.\)
Bảng biến thiên:
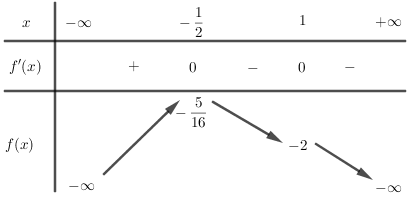
Suy ra hàm số đã cho nghịch biến trên khoảng \(\left( { - {\mkern 1mu} \dfrac{1}{2}; + {\mkern 1mu} \infty {\rm{\;}}} \right).\)

