Câu hỏi:
2 năm trước
Đề thi THPT QG 2019 – mã đề 104
Cho hàm số \(f\left( x \right)\) , bảng xét dấu của \(f'\left( x \right)\) như sau:
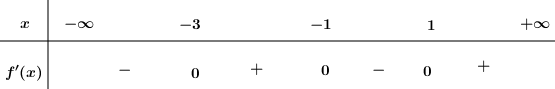
Hàm số \(y = f\left( {5 - 2x} \right)\) đồng biến trên khoảng nào dưới đây?
Trả lời bởi giáo viên
Đáp án đúng: b
Ta có \(y' = \left[ {f\left( {5 - 2x} \right)} \right]' = - 2f'\left( {5 - 2x} \right)\).
Xét \(y' > 0 \Leftrightarrow - 2f'\left( {5 - 2x} \right) > 0\) \( \Leftrightarrow f'\left( {5 - 2x} \right) < 0\)
\( \Leftrightarrow \left[ \begin{array}{l}5 - 2x < - 3\\ - 1 < 5 - 2x < 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x > 4\\2 < x < 3\end{array} \right.\)
=> Hàm số đồng biến trên \(\left( {2;3} \right)\) và \(\left( {4; + \infty } \right)\).
Hướng dẫn giải:
+) Tính \(y'\).
+) Giải bất phương trình \(y' > 0\).
Giải thích thêm:
Lưu ý khi tính đạo hàm hàm hợp: \(\left[ {f\left( u \right)} \right]' = u'.f'\left( u \right)\).
Câu hỏi khác
- Bài tập sự đồng biến, nghịch biến của hàm số toán 12 có lời giải
- Bài tập cực trị của hàm số toán 12 có lời giải
- Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số toán 12 có lời giải
- Bài tập cực trị có tham số đối với các hàm số cơ bản môn Toán lớp 12
- Bài tập đồ thị của hàm số và phép tịnh tiến hệ tọa độ toán 12 có lời giải
