Câu hỏi:
2 năm trước
Hàm số $y = - {\mkern 1mu} {x^4} + 2{x^3} - 2x - 1$ nghịch biến trên khoảng nào sau đây ?
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có \(y' = - {\mkern 1mu} 4{x^3} + 6{x^2} - 2;{\mkern 1mu} {\mkern 1mu} \forall x \in \mathbb{R}.\)
Khi đó \(y' = 0 \Leftrightarrow - 4{x^3} + 6{x^2} - 2 = 0\)\( \Leftrightarrow - 2{\left( {x - 1} \right)^2}\left( {2x + 1} \right) =0\Leftrightarrow \left[ \begin{array}{l}x = - {\mkern 1mu} \dfrac{1}{2}\\x = 1\end{array} \right.\)
Bảng biến thiên:
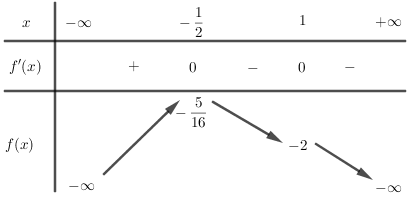
Suy ra hàm số đã cho nghịch biến trên khoảng \(\left( { - {\mkern 1mu} \dfrac{1}{2}; + {\mkern 1mu} \infty {\rm{\;}}} \right).\)
Hướng dẫn giải:
- Tính \(y'\).
- Tìm các nghiệm của đạo hàm \(y' = 0\).
- Xét dấu đạo hàm và kết luận.
Câu hỏi khác
- Bài tập sự đồng biến, nghịch biến của hàm số toán 12 có lời giải
- Bài tập cực trị của hàm số toán 12 có lời giải
- Bài tập giá trị lớn nhất và giá trị nhỏ nhất của hàm số toán 12 có lời giải
- Bài tập cực trị có tham số đối với các hàm số cơ bản môn Toán lớp 12
- Bài tập đồ thị của hàm số và phép tịnh tiến hệ tọa độ toán 12 có lời giải
