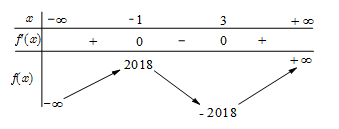Cô An đang ở khách sạn \(A\) bên bờ biển, cô cần đi du lịch đến hòn đảo \(C\). Biết rằng khoảng cách từ đảo \(C\) đến bờ biển là \(10\;{\rm{km}}\), khoảng cách từ khách sạn \(A\) đến điểm \(B\) trên bờ gần đảo \(C\) nhất là \(50\;{\rm{km}}\). Từ khách sạn \(A\), cô An có thể đi đường thủy hoặc đi đường bộ rồi đi đường thủy để đến hòn đảo \(C\) (như hình vẽ bên). Biết rằng chi phí đi đường thủy là \(5\) USD/km, chi phí đi đường bộ là \(3\)USD/km. Hỏi cô An phải đi đường bộ một khoảng bao nhiêu km để chi phí là nhỏ nhất.
Trả lời bởi giáo viên
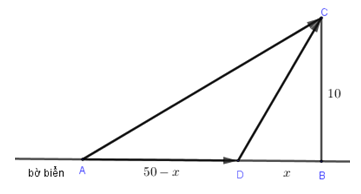
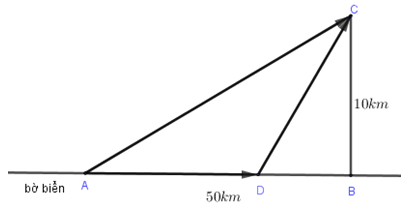
Gọi \(AD\) là quãng đường cô An đi đường bộ.
Đặt \(DB = x\,\left( {{\rm{km}}} \right)\left( {0 \le x \le 50} \right)\) \( \Rightarrow AD = 50 - x\,\left( {{\rm{km}}} \right)\).
Chi phí của cô An: \(f\left( x \right) = \left( {50 - x} \right)3 + \sqrt {{x^2} + {{10}^2}} {\rm{.5 }}\left( {{\rm{USD}}} \right)\)
\(f\left( x \right)\) liên tục trên \(\left[ {0;50} \right]\).
Ta có $f'\left( x \right) = - 3 + 5.\dfrac{{x{\rm{ }}}}{{\sqrt {{x^2} + 100} }}$$ = \dfrac{{ - 3\sqrt {{x^2} + 100} + 5x{\rm{ }}}}{{\sqrt {{x^2} + 100} }}$
$f'\left( x \right) = 0$$ \Leftrightarrow - 3\sqrt {{x^2} + 100} + 5x{\rm{ }} = 0$$ \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\9\left( {{x^2} + 100} \right) = 25{x^2}\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\{x^2} = \dfrac{{9.100}}{{16}}\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\x = \dfrac{{15}}{2}\end{array} \right.$.
Ta có \(f\left( 0 \right) = 200;\,\,f\left( {50} \right) = 50\sqrt {26} ;\,\,f\left( {\dfrac{{15}}{2}} \right) = 190\)
Để chi phí ít nhất thì $x = \dfrac{{15}}{2}$.
Vậy cô An phải đi đường bộ một khoảng: \(AD = 50 - \dfrac{{15}}{2} = \dfrac{{85}}{2}\left( {{\rm{km}}} \right)\) để chi phí ít nhất.
Hướng dẫn giải:
- Lập phương trình hàm số chỉ chi phí cô An đi bộ từ \(A\) đến \(D\) rồi lại đi đường thủy từ \(D\) đến \(B\)
- Tìm giá trị nhỏ nhất của hàm số trên và kết luận.