Cho hàm số \(y = {x^4} - 2m{x^2} + m\), có đồ thị \(\left( C \right)\) với \(m\) là tham số thực. Gọi \(A\) là điểm thuộc đồ thị \(\left( C \right)\) có hoành độ bằng \(1\). Tìm \(m\) để tiếp tuyến \(\Delta \) với đồ thị \(\left( C \right)\) tại \(A\) cắt đường tròn \(\left( \gamma \right):\,{x^2} + {\left( {y - 1} \right)^2} = 4\) tạo thành một dây cung có độ dài nhỏ nhất
Trả lời bởi giáo viên
Đường tròn \(\left( \gamma \right):\,{x^2} + {\left( {y - 1} \right)^2} = 4\) có tâm \(I\left( {0;\,1} \right)\), \(R = 2\)
Ta có \(A\left( {1;\,1 - m} \right)\); \(y' = 4{x^3} - 4mx \Rightarrow y'\left( 1 \right) = 4 - 4m\)
Suy ra phương trình \(\Delta \): \(y = \left( {4 - 4m} \right)\left( {x - 1} \right) + 1 - m\).
Dễ thấy \(\Delta \) luôn đi qua điểm cố định $F\left( {\dfrac{3}{4};\,0} \right)$ và điểm $F$ nằm trong đường tròn \(\left( \gamma \right)\)
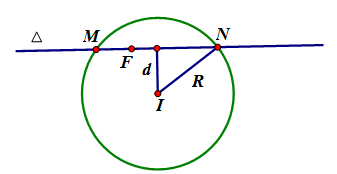
Giả sử \(\Delta \) cắt \(\left( \gamma \right)\) tại \(M\), \(N\). Thế thì ta có: \(MN = 2\sqrt {{R^2} - {d^2}\left( {I;\,\Delta } \right)} = 2\sqrt {4 - {d^2}\left( {I;\,\Delta } \right)} \)
Do đó \(MN\) nhỏ nhất $ \Leftrightarrow d\left( {I;\,\Delta } \right)$ lớn nhất $ \Leftrightarrow d\left( {I;\,\Delta } \right) = IF$$ \Rightarrow \Delta \bot IF$
Khi đó đường \(\Delta \) có 1 vectơ chỉ phương $\vec u \bot \overrightarrow {IF} = \left( {\dfrac{3}{4};\, - 1} \right)$; \(\vec u = \left( {1;\,\,4 - 4m} \right)\) nên ta có:
$\overrightarrow u .\overrightarrow {IF} = 0 \Leftrightarrow 1.\dfrac{3}{4} - \left( {4 - 4m} \right) = 0$$ \Leftrightarrow m = \dfrac{{13}}{{16}}$
Hướng dẫn giải:
- Viết phương trình tiếp tuyến của \(\left( C \right)\) tại \(A\)
- Nhận xét tính chất của tiếp tuyến (đi qua điểm cố định) và đánh giá độ dài lớn nhất của dây cung ứng với khoảng cách nhỏ nhất từ tâm đến dây.