Cho hàm số f(x) có đồ thị là đường cong (C), biết đồ thị của f′(x) như hình vẽ:
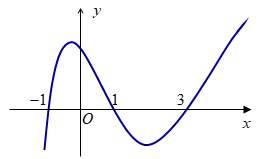
Tiếp tuyến của (C) tại điểm có hoành độ bằng 1 cắt đồ thị (C) tại hai điểm A, B phân biệt lần lượt có hoành độ a, b. Chọn khẳng định đúng trong các khẳng định sau:
Trả lời bởi giáo viên
Từ đồ thị, ta có f′(1)=0.
Phương trình tiếp tuyến của (C) tại điểm có hoành độ bằng 1 có dạng: y=f′(1)(x−1)+f(1)⇔y=f(1).
Phương trình hoành độ giao điểm của tiếp tuyến trên với đồ thị (C): f(x)=f(1).
Từ đồ thị, ta có f′(−1)=f′(3)=0. Ta được bảng biến thiên của hàm số y=f(x).
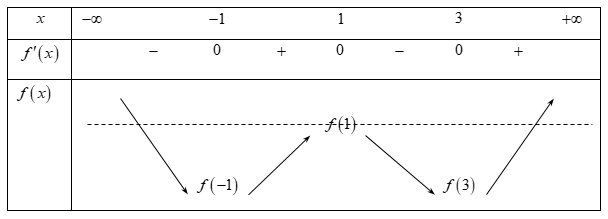
Từ bảng biến thiên, ta thấy đường thẳng y=f(1) cắt đồ thị hàm số tại ba điểm có hoành độ lần lượt là 1, a, b với a<−1 và b>3. Như vậy đáp án D đúng, các khẳng định A, B, C đều không thỏa điều trên.
Hướng dẫn giải:
- Viết phương trình tiếp tuyến của đồ thị hàm số (C) tại điểm có hoành độ 1
- Lập bảng biến thien của hàm số y=f(x) rồi suy ra kết luận đáp án đúng.