Cho điểm \(M\), đường tròn \(\left( {{C_M}} \right)\) trục \(\Delta \) và các điểm \(N \in \left( {{C_M}} \right),A \in \Delta \). Chọn mệnh đề sai:

Đường tròn $(C_M)$ là đường tròn đi qua điểm $M$.
Vì $N\in (C_M)$ nhưng \(MN\) chưa chắc là đường kính nên A sai.
Ngoài ra \(d\left( {M,\Delta } \right)=MO=NO = d\left( {N,\Delta } \right)\)
\(\Delta\) vuông góc với mp chứa \((C_M)\) nên vuông góc với mọi đường thẳng thuộc mp này.
Do đó \( \Delta \bot MN\)
Tam giác vuông AOM = AON (hai cạnh góc vuông) nên \(AM = AN\)
Vậy các đáp án còn lại đều đúng.
Cho hai điểm \(M,N\) và đường thẳng \(\Delta \). Chỉ cần điều kiện nào sau đây là đủ để tồn tại một đường tròn duy nhất đi qua cả \(M,N\) và nhận \(\Delta \) làm trục?
Đáp án A sai vì nếu \(d\left( {M,\Delta } \right) \ne d\left( {N,\Delta } \right)\) thì điểm \(M \notin \left( {{C_N}} \right)\) và \(N \notin \left( {{C_M}} \right)\) nên không có đường tròn thỏa mãn.
Đáp án B sai vì nếu \(d\left( {M,\Delta } \right) = d\left( {N,\Delta } \right)\) nhưng \(MN\) không vuông góc \(\Delta \) thì \(MN\) không thuộc đường tròn nhận \(\Delta \) làm trục.
Đáp án C sai vì chưa chắc \(MN\) có vuông góc \(\Delta \) hay không, hoặc \(d\left( {M,\Delta } \right)\) và \(d\left( {N,\Delta } \right)\) có bằng nhau hay không.
Đáp án D đúng vì gọi \(\left( {{C_M}} \right)\) là đường tròn qua \(M\) và nhận \(\Delta \) làm trục; gọi \(\left( P \right)\) là mặt phẳng đi qua \(M\) và vuông góc với \(\Delta \) thì \(\left( {{C_M}} \right) \subset \left( P \right)\)
Nếu \(MN \bot \Delta \) thì \(\left( P \right)\) đi qua \(N\).
Mặt khác \(d\left( {M,\Delta } \right) = d\left( {N,\Delta } \right)\) nên \(N\) nằm trên đường tròn \(\left( {{C_M}} \right)\).
Mặt tròn xoay không thể có được nếu quay hình nào quanh một đường thẳng?
Dựa vào định nghĩa ta thấy các đáp án A, B, C đều là các đường nên khi quay chúng quanh đường thẳng ta được mặt tròn xoay.
Đáp án D là một điểm nên khi quay ta chỉ được một đường tròn, do đó nó không là mặt tròn xoay.
Quay đường cong nào sau đây quanh trục đối xứng của nó ta sẽ được một mặt cầu?
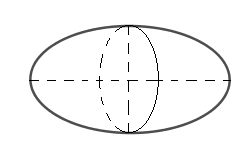
Đáp án A: Quay elip quanh trục đối xứng của nó ta được mặt tròn xoay nhưng không phải mặt cầu.
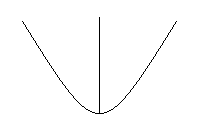
Đáp án B: Quay parabol quanh trục đối xứng của nó ta được mặt tròn xoay mà không phải mặt cầu.
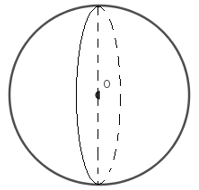
Đáp án C: Quay đường tròn quanh đường kính của nó ta được mặt cầu.
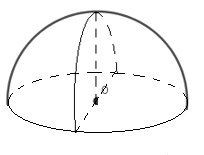
Đáp án D: Quay nửa đường tròn quanh trục đối xứng của nó ta chỉ được nửa mặt cầu.
Cho hai đường thẳng \(d\) và \(d'\) cắt nhau tại điểm \(O\) và góc giữa hai đường thẳng là \(\alpha \). Quay đường thẳng \(d'\) quanh \(d\) thì số đo \(\alpha \) bằng bao nhiêu để mặt tròn xoay nhận được là mặt nón tròn xoay?
Trong mặt phẳng \(\left( P \right)\) cho hai đường thẳng \(d,d'\) cắt nhau tại \(O\) và tạo thành góc \(\alpha \left( {{0^0} < \alpha < {{90}^0}} \right)\). Khi quay mặt phẳng \(\left( P \right)\) xung quanh \(d\) thì đường thẳng \(d'\) sinh ra một mặt được gọi là mặt nón tròn xoay (gọi tắt mặt nón).
Do đó điều kiện để có được mặt nón tròn xoay là góc \({0^0} < \alpha < {90^0}\).
Cho hai đường thẳng \(d\) và \(d'\) cắt nhau tại điểm \(O\) và góc giữa hai đường thẳng là \(\alpha \left( {{0^0} < \alpha < {{90}^0}} \right)\). Quay đường thẳng \(d'\) quanh \(d\) thì ta được mặt nón có góc ở đỉnh bằng:
\(\alpha \) là góc giữa hai đường thẳng \(d,d'\) thì góc \(2\alpha \) là góc ở đỉnh của mặt nón.
Cho tam giác $AOB$ vuông tại $O$. Quay tam giác quanh cạnh $OA$ ta được hình nón có đường sinh và đường cao lần lượt là:
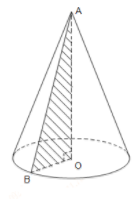
Quan sát hình vẽ ta thấy đường sinh là $AB$ và đường cao $AO$.
Cho tam giác $ABC$ vuông tại $A$, $AH$ là đường cao. Khi quay các cạnh của tam giác $ABC$ quanh cạnh $BC$ thì số hình nón được tạo thành là mấy hình?
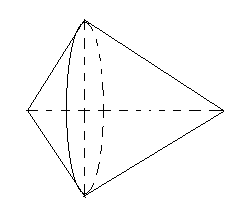
Quay tam giác vuông $ABC$ quanh cạnh huyền $BC$ ta được hai hình nón.
Hình $ABCD$ khi quay quanh $BC$ thì tạo ra:
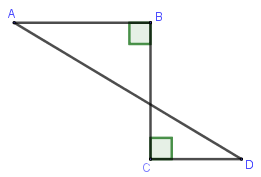

Gọi $O$ là giao điểm của $AD$ và $BC$.
- Quay tam giác vuông \(ABO\) quanh \(BO\) ta được một hình nón.
- Quay tam giác vuông \(DCO\) quanh \(CO\) ta được một hình nón.
Vậy có tất cả hai hình nón được tạo thành.
Cho hai đường thẳng \(d\) và \(\Delta \), điều kiện nào sau đây của \(d\) và \(\Delta \) thì khi quay \(d\) quanh \(\Delta \) ta được một mặt trụ?
Khi quay đường thẳng \(d\) quanh một đường thẳng \(\Delta //d\) thì ta được mặt trụ có trục \(\Delta \) và đường sinh \(d\).
Khi quay hình chữ nhật \(ABCD\) quanh các cạnh nào dưới đây ta được hai hình trụ có cùng chiều cao?
- Quay hình chữ nhật quanh một cạnh thì ta được hình trụ nên loại đáp án C và B vì có các đường chéo.
- Do \(AB \ne AD\) nên hai hình trụ tạo thành có chiều cao khác nhau.
- Do \(AD = BC\) nên hai hình trụ tạo thành có chiều cao bằng nhau.
Cho hình chữ nhật \(ABCD\), khi quay hình chữ nhật quanh cạnh \(AD\) thì \(CD\) được gọi là:
Quay hình chữ nhật \(ABCD\) quanh cạnh \(AD\) thì được hình trụ có chiều cao \(AD\), đường sinh \(BC\) và bán kính đáy \(AB,CD\).
Do đó \(CD\) được gọi là bán kính đáy.
Khi quay hình chữ nhật \(MNPQ\) quanh đường thẳng \(AB\) với \(A,B\) lần lượt là trung điểm của \(MN,PQ\) ta được một hình trụ có đường kính đáy:
Hình trụ tạo thành khi quay hình chữ nhật \(MNPQ\) quanh đường trung bình \(AB\) ta sẽ được hình trụ có đường cao \(AB\), đường sinh \(MQ,NP\) và bán kính đáy \(MA,NA,BP,BQ\), đường kính đáy \(MN,PQ\).
Do đó đường kính đáy của hình trụ là \(MN\).
Nếu cắt mặt trụ bởi mặt phẳng vuông góc với trục ta được là:
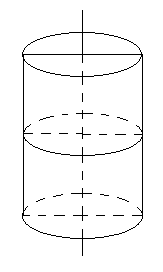
Khi cắt mặt trụ bởi mặt phẳng vuông góc với đáy ta được đường tròn có bán kính bằng bán kính mặt trụ.
Nếu cắt mặt trụ tròn xoay bởi một mặt phẳng tạo với trục một góc \(\alpha \left( {{0^0} < \alpha < {{90}^0}} \right)\) thì ta được:
Khi cắt mặt trụ bởi mặt phẳng tạo với trục một góc \(\alpha \left( {{0^0} < \alpha < {{90}^0}} \right)\) thì ta được elip.
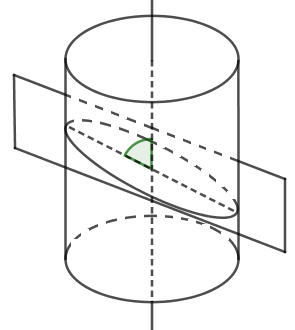
Cho hình trụ có trục \(\Delta \) và bán kính \(R\). Khi cắt hình trụ bởi mặt phẳng \(\left( \alpha \right)\) song song với \(\Delta \) và cách \(\Delta \) một khoảng \(d\left( {\Delta ;\left( \alpha \right)} \right) = k < R\) thì ta được thiết diện là:
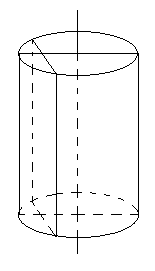
Khi cắt hình trụ bởi mặt phẳng song song với trục mà khoảng cách giữa \(\left( \alpha \right)\) và trục nhỏ hơn bán kính hình trụ thì ta được thiết diện là hình chữ nhật.
Khi quay hình vẽ dưới đây quanh trục đối xứng là đường thẳng \(d\) thì ta được:
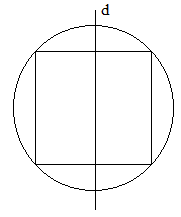
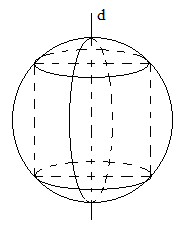
Quan sát hình vẽ ta thấy, khi quay hình vẽ ban đầu quanh đường thẳng \(d\) thì ta được hình trụ nội tiếp hình cầu hoặc hình cầu ngoại tiếp hình trụ.
Cho hình vẽ sau, chọn mệnh đề sai:
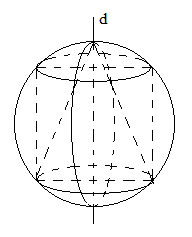
Quan sát hình vẽ ta thấy hình trụ nội tiếp mặt cầu, hình nón nội tiếp mặt cầu, mặt cầu ngoại tiếp hình nón nên các đáp án A, C và D đúng.
Ngoài ra hình nón không nội tiếp hình trụ vì hình trụ không đi qua đỉnh hình nón.

