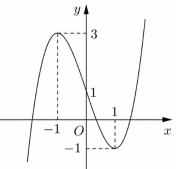
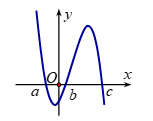
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên.
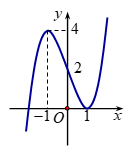
Phương trình \(\left| {f\left( {x - 2} \right) - 2} \right| = \pi \) có bao nhiêu nghiệm thực phân biệt?
Trả lời bởi giáo viên
Cách 1:
+ Tịnh tiến đồ thị \(y = f\left( x \right)\) sang phải $2$ đơn vị ta được đồ thị hàm số \(y = f\left( {x - 2} \right)\) (hình a)
+ Tịnh tiến đồ thị \(y = f\left( {x - 2} \right)\) xuống dưới $2$ đơn vị ta được đồ thị hàm số \(y = f\left( {x - 2} \right) - 2\) (hình b)
+ Vẽ đồ thị hàm số \(y = \left| {f\left( {x - 2} \right) - 2} \right|\) như hình c.
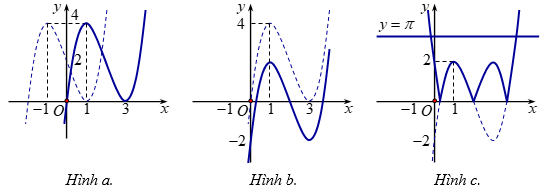
Dựa vào đồ thị hàm số \(y = \left| {f\left( {x - 2} \right) - 2} \right|\) suy ra phương trình \(\left| {f\left( {x - 2} \right) - 2} \right| = \pi \) có hai nghiệm thực phân biệt.
Hướng dẫn giải:
- Dựng đồ thị hàm số \(y = \left| {f\left( {x - 2} \right) - 2} \right|\) dựa vào đồ thị hàm số \(y = f\left( x \right)\) đã cho.
- Số nghiệm của phương trình bằng số giao điểm của hai đồ thị hàm số.