Cho các số thực dương \(x\), \(y\). Tìm giá trị lớn nhất của biểu thức \(P = \dfrac{{4x{y^2}}}{{{{\left( {x + \sqrt {{x^2} + 4{y^2}} } \right)}^3}}}\)
Trả lời bởi giáo viên
\(P = \dfrac{{4x{y^2}}}{{{{\left( {x + \sqrt {{x^2} + 4{y^2}} } \right)}^3}}} = \dfrac{{4{{\left( {\dfrac{y}{x}} \right)}^2}}}{{{{\left( {1 + \sqrt {1 + 4{{\left( {\dfrac{y}{x}} \right)}^2}} } \right)}^3}}}\) \(\left( {\forall x >0,y > 0} \right)\)
Đặt \(t = \sqrt {1 + 4{{\left( {\dfrac{y}{x}} \right)}^2}} \), \(t > 1\). Khi đó biểu thức trở thành \(P\left( t \right) = \dfrac{{{t^2} - 1}}{{{{\left( {t + 1} \right)}^3}}}=\dfrac{{t - 1}}{{{{\left( {t + 1} \right)}^2}}}\) với \(t > 1\)
\(P'\left( t \right) = \dfrac{{ - {t^2} + 2t + 3}}{{{{\left( {t + 1} \right)}^4}}} = 0 \Leftrightarrow t = 3\)
Bảng biến thiên:
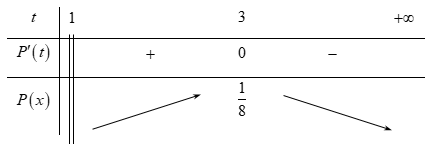
Vậy $\max P = P\left( 3 \right) = \dfrac{1}{8}$.
Hướng dẫn giải:
- Chia cả tử và mẫu của \(P\) cho \({x^3} \ne 0\)
- Đặt ẩn phụ, tìm điều kiện cho ẩn phụ, đưa về hàm số \(1\) biến.
- Xét hàm tìm \(\max ,\min \) và kết luận.