Nhà xe khoán cho hai tài xế ta-xi An và Bình mỗi người lần lượt nhận $32$ lít và $72$ lít xăng. Hỏi tổng số ngày ít nhất là bao nhiêu để hai tài xế chạy tiêu thụ hết số xăng của mình được khoán, biết rằng chỉ tiêu cho hai người một ngày tổng cộng chỉ chạy đủ hết $10$ lít xăng?
Trả lời bởi giáo viên
Gọi $x$ là số lít xăng mà An đã dùng trong một ngày. Với $0 < x < 10$.
$ \Rightarrow $ $10 - x$ là số lít xăng mà Bình đã dùng trong một ngày.
Khi đó
+ Để An tiêu thụ hết $32$ lít xăng cần $\dfrac{{32}}{x}$ ngày.
+ Để Bình tiêu thụ hết $72$ lít xăng cần $\dfrac{{72}}{{10 - x}}$ ngày.
Vậy tổng số ngày chạy xe của hai tài xế là
$y = \dfrac{{32}}{x} + \dfrac{{72}}{{10 - x}} \Rightarrow y' = - \dfrac{{32}}{{{x^2}}} + \dfrac{{72}}{{{{\left( {10 - x} \right)}^2}}} \Rightarrow y' = 0 \Leftrightarrow x = 4$
Bảng biến thiên:
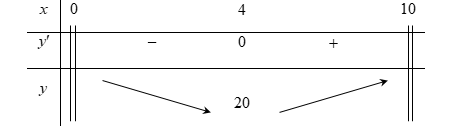
Nhìn bảng biến thiên ta thấy tổng số ngày chạy xe ít nhất của hai tài xế là \(20\) ngày.
Hướng dẫn giải:
- Đặt số lít xăng tiêu thụ mỗi ngày của An là \(x\), chú ý điều kiện của \(x\)
- Viết hàm số biểu thị tổng số ngày cả hai người dùng hết để tiêu thụ hết xăng.
- Tìm GTNN của hàm số và kết luận.