Cho mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {z^2} = 9\) và mặt phẳng \(\left( Q \right):x - y + z - 1 = 0\). Hai điểm \(M\) và \(N\) lần lượt di động trên mặt cầu \(\left( S \right)\) và mặt phẳng \(\left( Q \right)\). Xác định vector \(\overrightarrow {MN} \) khi \(MN\) đạt giá trị lớn nhất và vuông góc với mặt phẳng \(\left( Q \right)\).

Mặt cầu \(\left( S \right)\) có tâm là \(I\left( {1;2;0} \right)\) và bán kính là \(R = 3\) \( \Rightarrow {d_{\left( {I,\left( Q \right)} \right)}} = \dfrac{2}{{\sqrt 3 }} < R\)

\( \Rightarrow \) Mặt cầu \(\left( S \right)\) cắt \(\left( Q \right)\) và tâm \(I\) không thuộc mặt phẳng \(\left( Q \right)\).

Ta có hình vẽ minh họa như sau:

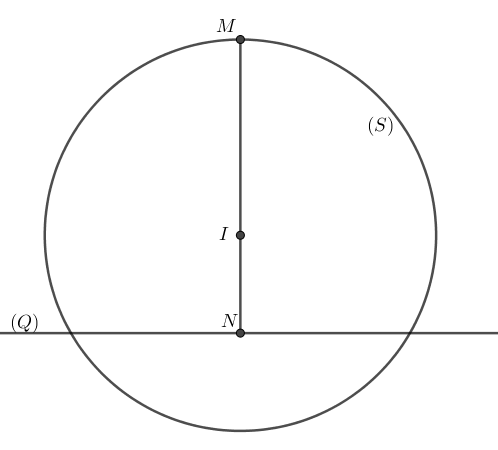
Vẽ hình, ta xác định được độ dài \(MN\) lớn nhất đồng thời vuông góc với mặt phẳng \(\left( Q \right)\) như hình vẽ trên.

\( \Rightarrow \) \(I,M,N\) thẳng hàng.

Khi đó, \(MN:\left\{ \begin{array}{l}\overrightarrow u  = \overrightarrow {{n_{\left( Q \right)}}}  = \left( {1; - 1;1} \right)\\I\left( {1;2;0} \right) \in MN\end{array} \right.\) \( \Rightarrow MN:\dfrac{{x - 1}}{1} = \dfrac{{y - 2}}{{ - 1}} = \dfrac{z}{1}\).

\( \Rightarrow \left\{ \begin{array}{l}M\left( {1 + t;2 - t;t} \right) \in \left( S \right)\\N\left( {1 + u;2 - u;u} \right) \in \left( Q \right)\end{array} \right.\)

\( \Rightarrow \left\{ \begin{array}{l}{\left( {1 + t - 1} \right)^2} + {\left( {2 - t - 2} \right)^2} + {t^2} = 9\\1 + u - \left( {2 - u} \right) + u - 1 = 0\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}t = \sqrt 3 \\t =  - \sqrt 3 \end{array} \right.\\u = \dfrac{2}{3}\end{array} \right.\)\( \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}N\left( {\dfrac{5}{3};\dfrac{4}{3};\dfrac{2}{3}} \right)\\{M_1}\left( {1 + \sqrt 3 ;2 - \sqrt 3 ;\sqrt 3 } \right)\end{array} \right.\\\left\{ \begin{array}{l}N\left( {\dfrac{5}{3};\dfrac{4}{3};\dfrac{2}{3}} \right)\\{M_2}\left( {1 - \sqrt 3 ;2 + \sqrt 3 ; - \sqrt 3 } \right)\end{array} \right.\end{array} \right.\)\( \Rightarrow \left[ \begin{array}{l}\overrightarrow {{M_1}N} \left( {\dfrac{2}{3} - \sqrt 3 ;\sqrt 3  - \dfrac{2}{3};\dfrac{2}{3} - \sqrt 3 } \right)\\\overrightarrow {{M_2}N} \left( {\dfrac{2}{3} + \sqrt 3 ; - \sqrt 3  - \dfrac{2}{3};\dfrac{2}{3} + \sqrt 3 } \right)\end{array} \right.\)

Dễ dàng kiểm tra được \({M_2}N > {M_1}N\)

\( \Rightarrow \overrightarrow {MN}  = \overrightarrow {{M_2}N}  = \left( {\dfrac{2}{3} + \sqrt 3 ; - \sqrt 3  - \dfrac{2}{3};\dfrac{2}{3} + \sqrt 3 } \right)\)