Cho số phức \(z\) thỏa mãn \(\left\{ {\begin{array}{*{20}{l}}{|z - 1 - 2i| \le 1}\\{|z - 1 + 2i| \ge |z + 3 - 2i|}\end{array}.} \right.\) Gọi \(S\) là diện tích phần mặt phẳng chứa các điểm biểu diễn của số phức \(z\). Tính \(S\).

Bước 1: Giả sử \(z = x + yi(x,y \in \mathbb{R})\). Giải \(|z - 1 - 2i| \le 1\)

Giả sử \(z = x + yi(x,y \in \mathbb{R})\). Khi đó

\(|z - 1 - 2i| \le 1\) \( \Leftrightarrow |(x - 1) + (y - 2)i| \le 1\)\( \Leftrightarrow \sqrt {{{(x - 1)}^2} + {{(y - 2)}^2}}  \le 1\)\( \Leftrightarrow {(x - 1)^2} + {(y - 2)^2} \le 1\)

Bước 2: Giải \(|z - 1 + 2i| \ge |z + 3 - 2i|\)

Và \(|z - 1 + 2i| \ge |z + 3 - 2i|\) \( \Leftrightarrow \sqrt {{{(x - 1)}^2} + {{(y + 2)}^2}} \)\( \ge \sqrt {{{(x + 3)}^2} + {{(y - 2)}^2}} \)

\( \Leftrightarrow {(x - 1)^2} + {(y + 2)^2}\)\( \ge {(x + 3)^2} + {(y - 2)^2}\)\( \Leftrightarrow y \ge x + 1\)

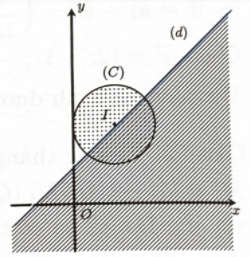
Bước 3: Gọi \((T)\) là nửa mặt phẳng có bờ là đường thẳng \(d:y = x + 1\), không chứa gốc tọa độ \(O(0;0)\). Tính S.

Gọi \((T)\) là nửa mặt phẳng có bờ là đường thẳng \(d:y = x + 1\), không chứa gốc tọa độ \(O(0;0)\). Khi đó tập hợp các điểm biểu diễn số phức \(z\) thỏa mãn đề là nửa hình tròn \((C)\) tâm \(I(1;2)\), bán kính \(R = 1\) và thuộc \((T)\). Vì đường thẳng \(d\) đi qua tâm \(I(1;2)\) của hình tròn \((C)\) nên diện tích cần tìm là một nửa diện tích hình tròn \((C)\). Do đó \(S = \dfrac{\pi }{2}\).