Bài toán liên quan đến điểm biểu diễn số phức thỏa mãn điều kiện cho trước

Giả sử $z = a + bi{\rm{ }}\left( {a;{\rm{ }}b \in \mathbb{R}} \right) \Rightarrow \bar z = a - bi.$

Theo giả thiết, ta có $\left( {a + bi} \right) - \left( {a - bi} \right) = {\left( {a + bi} \right)^2} \Leftrightarrow 2bi = {a^2} - {b^2} + 2abi$

$ \Leftrightarrow \left( {{a^2} - {b^2}} \right) + \left( {2ab - 2b} \right)i = 0 \Leftrightarrow \left\{ \begin{array}{l}{a^2} - {b^2} = 0\\2ab - 2b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}a = b\\a =  - b\end{array} \right.\\2ab - 2b = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a = b = 0\\a = b = 1\\a = 1;\,b =  - 1\end{array} \right..$

Vậy có 3 số phức thỏa mãn là $z = 0$, $z = 1 + i$ và $z = 1 - i$.

Từ giả thiết, ta có \(OA = 3,{\rm{ }}OB = 4\) và \(AB = 5\).

Ta có \(O{A^2} + O{B^2} = A{B^2}\) \( \Rightarrow \Delta OAB\) vuông tại \(O.\)

Vậy \(S = \dfrac{1}{2}OA.OB = \dfrac{1}{2}.3.4 = 6\).

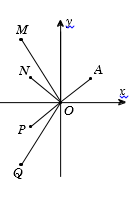
Gọi \(z = x + yi{\rm{ }}\left( {x;{\rm{ }}y \in \mathbb{R}} \right).\) Từ giả thiết, ta có \(\left\{ \begin{array}{l}{x^2} + {y^2} = 1\\x > 0;{\rm{ }}y > 0\end{array} \right..\)

Ta có $w = \dfrac{1}{{iz}} =  - \dfrac{i}{z} =  - \dfrac{i}{{x + yi}} =  - \dfrac{{i\left( {x - yi} \right)}}{{\left( {x + yi} \right)\left( {x - yi} \right)}} =  - \dfrac{{y + xi}}{{{x^2} + {y^2}}} =  - \,y - xi.$

Vì $x > 0,{\rm{ }}y > 0$ nên điểm biểu diễn số phức $w$ có tọa độ là $\left( { - \,y; - \,x} \right)$ (đều có hoành độ và tung độ âm). Đồng thời $\left| w \right| = \sqrt {{{\left( { - y} \right)}^2} + {{\left( { - x} \right)}^2}}  = 1 = \left| z \right|.$ Suy ra điểm biểu diễn của số phức $w$ nằm trong góc phần tư thứ III và cách gốc tọa độ \(O\) một khoảng bằng \(OA.\) Quan sát hình vẽ ta thấy có điểm \(P\) thỏa mãn.

Số phức \(z = 2 + 5i\) có điểm biểu diễn là \(A\) suy ra \(A\left( {2;5} \right)\).

Số phức \(z =  - 2 + 5i\) có điểm biểu diễn là \(B\) suy ra \(B\left( { - 2;5} \right)\).

Do đó \(\left\{ \begin{array}{l}{x_A} =  - {x_B}\\{y_A} = {y_B}\end{array} \right.\) nên \(A\) và \(B\) đối xứng nhau qua trục tung

Số phức \(z = 4 - 7i\) có điểm biểu diễn là \(A\) suy ra \(A\left( {4; - 7} \right)\).

Số phức \(z' =  - 4 + 7i\) có điểm biểu diễn là \(B\) suy ra \(B\left( { - 4;7} \right)\).

Do đó \(\left\{ \begin{array}{l}{x_A} + {x_B} = 0\\{y_A} + {y_B} = 0\end{array} \right.\) nên \(A\) và \(B\) đối xứng nhau qua gốc tọa độ \(O\).

Số phức \(z = 3 + 2i\) có điểm biểu diễn là \(A\) suy ra \(A\left( {3;2} \right)\).

Số phức \(z' = 2 + 3i\) có điểm biểu diễn là \(B\) suy ra \(B\left( {2;3} \right)\).

Ta thấy \(\left\{ \begin{array}{l}{x_A} = {y_B}\\{y_A} = {x_B}\end{array} \right.\) nên hai điểm \(A\) và \(B\) đối xứng nhau qua đường thẳng \(y = x\).

+) Vì \(\dfrac{{1 - i}}{{\bar z}}\) là số thực với \(z = a + bi\) nên tồn tại số thực \(k(k \ne 0)\) sao cho

\(\begin{array}{l}\bar z = k(1 - i) \Leftrightarrow a - bi = k - ki\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = k}\\{ - b =  - k}\end{array} \Rightarrow a = b(1)} \right.\end{array}\).

+) \(|z - 3i| - |z - 3 - 2i| = 2\)\( \Leftrightarrow \sqrt {{a^2} + {{(b - 3)}^2}} \)\( - \sqrt {{{(a - 3)}^2} + {{(b - 2)}^2}}  = 2\) (2).

Thế \((1)\) vào \((2)\) ta được:

\(\sqrt {{b^2} + {{(b - 3)}^2}}  - \)\(\sqrt {{{(b - 3)}^2} + {{(b - 2)}^2}}  = 2\)

\( \Leftrightarrow \sqrt {{b^2} + {{(b - 3)}^2}} \)\( = 2 + \sqrt {{{(b - 3)}^2} + {{(b - 2)}^2}} \)

\( \Leftrightarrow 2{b^2} - 6b + 9 = 4 + 2{b^2}\)\( - 10b + 13 + 4\sqrt {2{b^2} - 10b + 13} \)\( \Leftrightarrow 4b - 8 = 4\sqrt {2{b^2}}  - 10b + 13\)

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b - 2 \ge 0}\\{{{(b - 2)}^2} = \left( {2{b^2} - 10b + 13} \right)}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b \ge 2}\\{{b^2} - 6b + 9 = 0}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b \ge 2}\\{b = 3}\end{array} \Leftrightarrow b = 3 \Rightarrow a = 3.} \right.\)

 \( \Rightarrow T = {3^2} + {3^2} = 18\).

Ta có:

\({z^2} - z + 1 - i\)\( = \left( {{z^2} - 2z + 2} \right) + (z - 1 - i)\)\( = (z - 1 - i)(z - 1 + i) + (z - 1 - i)\)\( = (z - 1 - i)(z + i)\)

Mặt khác \(\left\{ {\begin{array}{*{20}{l}}{|z - 1 - i| \ge 2}\\{\left| {{z^2} - z + 1 - i} \right| \le 4}\end{array}(*)} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{|z - 1 - i| \ge 2}\\{|(z - 1 - i)(z + i)| \le 4}\end{array}} \right.\)\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{|z - 1 - i| \ge 2}\\{|z + i| \le 2}\end{array}\quad (**)} \right.\).

Xét \(|z - 1 - i| \ge 2\) có tập hợp điểm biểu diễn số phức \(z\) là miền ngoài hình tròn (kể cả biên) \(\left( {{C_1}} \right)\) có \({I_1}(1;1),{R_1} = 2\).

Xét \(|z + i| \le 2\) có tập hợp điểm biểu diễn số phức \(z\) là miền trong hình tròn (kể cả biên) \(\left( {{C_2}} \right)\) có \({I_2}(0; - 1),{R_2} = 2\).

\( \Rightarrow \) Tát cả các điểm biểu diễn số phức \(z\) thỏa mãn \((**)\) là miền tô đậm như hình vẽ.

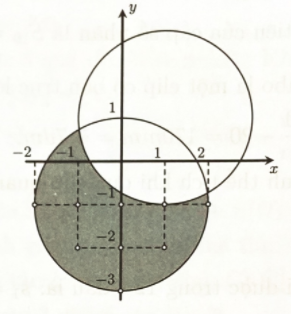
Do đó có 10 điểm có tọa độ nguyên thỏa mãn \((**)\) là:

\(( - 2; - 1),( - 1;0),( - 1; - 1),( - 1; - 2),\)\((0; - 1),(0; - 2),(0; - 3),(1; - 1),\)\((1; - 2),(2; - 1)\).

Thử lại vào điều kiện \((*)\) ta được 5 điểm thoả mãn là:

\(( - 1;0),( - 1; - 1),(0; - 1),(0; - 2),(1; - 1)\).

Vậy có tất cả 5 số phức \(z\) thỏa mãn đề bài.

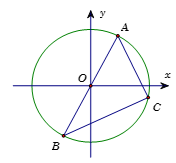
Giả sử \(\left| {{z_1}} \right| = \left| {{z_2}} \right| = \left| {{z_3}} \right| = R.\)

Khi đó \(A,{\rm{ }}B,{\rm{ }}C\) nằm trên đường tròn \(\left( {O;R} \right)\).

Do \({z_1} + {z_2} = 0\) nên hai điểm \(A,{\rm{ }}B\) đối xứng nhau qua \(O.\) Như vậy điểm \(C\) nằm trên đường tròn đường kính \(AB\) (bỏ đi hai điểm \(A\) và \(B\)) hay tam giác \(ABC\) vuông tại \(C\).

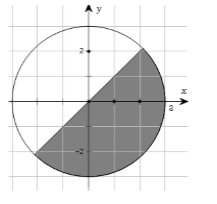
Gọi \(z = x + yi{\rm{ }}\left( {x;{\rm{ }}y \in \mathbb{R}} \right)\) và \(M\left( {x;y} \right)\) biểu diễn \(z\) trên mặt phẳng tọa độ.

Phần tô đậm là phần nằm dưới đường thẳng \(y=x\) và trong đường tròn tâm O bán kính 3 nên tọa độ của M thỏa mãn:

 \(\left\{ \begin{array}{l}{x^2} + {y^2} \le 9\\y \le x\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\sqrt {{x^2} + {y^2}}  \le 3\\y \le x\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\left| z \right| \le 3\\y \le x\end{array} \right..\)

Có \(\left\{ \begin{array}{l}{x_G} = \dfrac{{4 + 1 + 1}}{3} = 2\\{y_G} = \dfrac{{0 + 4 - 1}}{3} = 1\end{array} \right. \Rightarrow G(2;1) \Rightarrow z = 2 + i\)

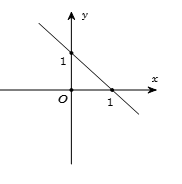
\(\Delta \) đi qua hai điểm \(\left( {1;0} \right)\) và \(\left( {0;1} \right)\) nên có phương trình $\Delta :x + y - 1 = 0$.

Khi đó ${\left| z \right|_{\min }} = d\left[ {O,\Delta } \right] = \dfrac{{\left| { - 1} \right|}}{{\sqrt {{1^2} + {1^2}} }} = \dfrac{1}{{\sqrt 2 }}.$

Giả sử ta có số phức $z = a + bi$ . Thay vào \({z^2} = {(\bar z)^2}\) có

\({(a + bi)^2} = {(a - bi)^2} \Leftrightarrow {a^2} - {b^2} + 2abi = {a^2} - {b^2} - 2abi \Leftrightarrow 2abi =  - 2abi \Leftrightarrow 2ab =  - 2ab \Leftrightarrow ab = 0.\)

Suy ra $a = 0$ hoặc $b = 0$ .

Giả sử ta có số phức $z = x + yi$ . Ta có \({z^2} = {(x + yi)^2} = {x^2} - {y^2} + 2xyi\).

\({z^2}\) là số thực âm \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x^2} - {y^2} < 0}&{}\\{xy = 0}&{}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 0}&{}\\{y \ne 0}&{}\end{array}} \right..\)

Giả sử ta có số phức $z = x + yi$.

Thay vào điều kiện \(|z(i + 1) - 1 - i| = \sqrt 2 \) có

\(|(x + yi)(i + 1) - 1 - i| = \sqrt 2  \Leftrightarrow |(x - y - 1) + (x + y - 1)i| = \sqrt 2  \Leftrightarrow \sqrt {{{(x - y - 1)}^2} + {{(x + y - 1)}^2}}  = \sqrt 2 \) \( \Leftrightarrow {(x - y - 1)^2} + {(x + y - 1)^2} = 2 \Leftrightarrow {(x - 1)^2} + {y^2} - 2(x - 1)y + {(x - 1)^2} + {y^2} + 2(x - 1)y = 2\) \( \Leftrightarrow 2{(x - 1)^2} + 2{y^2} = 2 \Leftrightarrow {(x - 1)^2} + {y^2} = 1\)

Giả sử ta có số phức $z = x + yi$. Thay vào điều kiện \(2|z - 1 - 2i| = |3i + 1 - 2\bar z|\) có

\(2|(x + yi) - 1 - 2i| = |3i + 1 - 2(x - yi)| \Leftrightarrow 2|(x - 1) + (y - 2)i| = |(1 - 2x) + (3 + 2y)i|\) \( \Leftrightarrow 2\sqrt {{{(x - 1)}^2} + {{(y - 2)}^2}}  = \sqrt {{{(1 - 2x)}^2} + {{(3 + 2y)}^2}} \)

\( \Leftrightarrow 4{(x - 1)^2} + 4{(y - 2)^2} = {(1 - 2x)^2} + {(3 + 2y)^2}\)

\( \Leftrightarrow 4{x^2} - 8x + 4 + 4{y^2} - 16y + 16 = 4{x^2} - 4x + 1 + 4{y^2} + 12y + 9\)

\( \Leftrightarrow 4x + 28y - 10 = 0\)

\( \Leftrightarrow 2x + 14y - 5 = 0\)

Giả sử $z = a + bi$ , ta có \({z^2} = {(a + bi)^2} = {a^2} - {b^2} + 2abi\).

Số phức \({z^2}\) có điểm biểu diễn nằm trên trục tung khi \({a^2} - {b^2} = 0 \Leftrightarrow a =  \pm b\).

Giả sử $z = a + bi$ , ta có \({z^2} = {(a + bi)^2} = {a^2} - {b^2} + 2abi\).

Số phức \({z^2}\) có điểm biểu diễn nằm trên trục hoành khi \(2ab = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{a = 0}\\{b = 0}\end{array}} \right..\)

Ta có \(w = \dfrac{{5 + iz}}{{1 + z}} \Leftrightarrow w\left( {1 + z} \right) = 5 + iz \Leftrightarrow w + wz = 5 + iz \Leftrightarrow z\left( {w - i} \right) = 5 - w\).

Nếu \(w = i \Leftrightarrow 0.z = 5 - i \Leftrightarrow 0 = 5 - i\) (vô lý) \( \Rightarrow w \ne i\)\( \Rightarrow z = \dfrac{{5 - w}}{{w - i}}\).

Theo bài ra ta có:

\(\left| z \right| = \sqrt 2  \Leftrightarrow \left| {\dfrac{{5 - w}}{{w - i}}} \right| = \sqrt 2  \Leftrightarrow \left| {5 - w} \right| = \sqrt 2 \left| {w - i} \right|\).

Đặt \(w = x + yi\) ta có: \(\left| {5 - x - yi} \right| = \sqrt 2 \left| {x + yi - i} \right|\).

\(\begin{array}{l} \Leftrightarrow {\left( {5 - x} \right)^2} + {y^2} = 2\left[ {{x^2} + {{\left( {y - 1} \right)}^2}} \right]\\ \Leftrightarrow {x^2} - 10x + 25 + {y^2} = 2{x^2} + 2{y^2} - 4y + 2\\ \Leftrightarrow {x^2} + {y^2} + 10x - 4y - 23 = 0\end{array}\)   

Ta có \({a^2} + {b^2} - c = {5^2} + {2^2} + 23 = 52 > 0 \Rightarrow \) Tập hợp các điểm biểu diễn số phức \(w\) là một đường tròn có bán kính \(R = \sqrt {{a^2} + {b^2} - c}  = \sqrt {52}  = 2\sqrt {13} \).

Giả sử ta có số phức $z = x + yi$ . Thay vào điều kiện \(|z - v| = 1\) ta có

\(|x + yi - (a + bi)| = 1 \Leftrightarrow |(x - a) + (y - b)i| = 1 \Leftrightarrow {(x - a)^2} + {(y - b)^2} = 1\)