Tập hợp các điểm trên mặt phẳng tọa độ $Oxy$ biểu diễn số phức $z$ thỏa mãn điều kiện: số phức \(w = (z - i)(2 + i)\) là một số thuần ảo là:
Giả sử ta có số phức $z = x + yi$ .
Ta có \(w = (x + yi - i)(2 + i) = (2x + 1 - y) + (x + 2y - 2)i\)
$w$ thuần ảo khi $2x + 1 - y = 0$.
Cho số phức \(z\) có \(|z| = 4\). Tập hợp các điểm \(M\) trong mặt phẳng tọa độ \(Oxy\) biểu diễn số phức \(w = \bar z + 3i\) là một đường tròn. Tính bán kính đường tròn đó.
Giả sử $w = a + bi$ . Ta có \(w = \bar z + 3i \Leftrightarrow a + bi = \bar z + 3i \Leftrightarrow \bar z = a + (b - 3)i.\)
Theo giả thiết \(|z| = 4 \Leftrightarrow |\bar z| = 4 \Leftrightarrow {a^2} + {(b - 3)^2} = {4^2}\)
Tập hợp các điểm $M$ trong mặt phẳng tọa độ $Oxy$ biểu diễn số phức $w$ là một đường tròn có bán kính bằng $4$.
Trong mặt phẳng phức, tập hợp các điểm biểu diễn của số phức $z$ thỏa mãn điều kiện \(2|z - i| = |z - \bar z + 2i|\) là
Giả sử ta có số phức $z = x + yi$. Thay vào điều kiện \(2|z - i| = |z - \bar z + 2i|\) có
\(2|(x + yi) - i| = |(x + yi) - (x - yi) + 2i| \Leftrightarrow 2|x + (y - 1)i| = |2(y + 1)i| \Leftrightarrow 2\sqrt {{x^2} + {{(y - 1)}^2}} = \sqrt {4{{(y + 1)}^2}} \) \( \Leftrightarrow 4{x^2} + 4{(y - 1)^2} = 4{(y + 1)^2} \Leftrightarrow 4{x^2} + 4{y^2} - 8y + 4 = 4{y^2} + 8y + 4 \Leftrightarrow 4{x^2} = 16y \Leftrightarrow {x^2} = 4y\)
Tập hợp các điểm \(M\) biểu diễn số phức $z$ thỏa mãn \(\left| {z - i} \right| + \left| {z + i} \right| = 4\) là:
Gọi $z = x + yi\,\,\,\left( {x;{\rm{ }}y \in \mathbb{R}} \right).$
Ta có \(\left| {z - i} \right| + \left| {z + i} \right| = 4 \Leftrightarrow \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} + \sqrt {{x^2} + {{\left( {y + 1} \right)}^2}} = 4\)
\( \Leftrightarrow \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} = 4 - \sqrt {{x^2} + {{\left( {y + 1} \right)}^2}} \Leftrightarrow \left\{ \begin{array}{l}\sqrt {{x^2} + {{\left( {y + 1} \right)}^2}} \le 4\\{x^2} + {\left( {y - 1} \right)^2} = 16 + {x^2} + {\left( {y + 1} \right)^2} - 8\sqrt {{x^2} + {{\left( {y + 1} \right)}^2}} \end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}{x^2} + {\left( {y + 1} \right)^2} \le 16\\2\sqrt {{x^2} + {{\left( {y + 1} \right)}^2}} = y + 4\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x^2} + {\left( {y + 1} \right)^2} \le 16\\y \ge - 4\\4{x^2} + 3{y^2} = 12\end{array} \right.\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x^2} + {{\left( {y + 1} \right)}^2} \le 16}&{\left( 1 \right)}\\{y \ge - 4}&{\left( 2 \right)}\\{\dfrac{{{x^2}}}{3} + \dfrac{{{y^2}}}{4} = 1}&{\left( 3 \right)}\end{array}} \right.\)
Tập hợp các điểm thỏa mãn \(\left( 3 \right)\) đều thỏa mãn \(\left( 1 \right)\) và \(\left( 2 \right)\).
Vậy tập hợp những điểm \(M\) là elip \(\left( E \right):\dfrac{{{x^2}}}{3} + \dfrac{{{y^2}}}{4} = 1.\)
Tìm tập hợp các điểm biểu diễn số phức \(z,\) biết rằng số phức \({z^2}\) có điểm biểu diễn nằm trên trục hoành.
Bước 1:
Giả sử \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\) ta có: \({z^2} = {\left( {a + bi} \right)^2} = {a^2} - {b^2} + 2abi.\)
Bước 2:
Số phức \({z^2}\) có điểm biểu diễn nằm trên trục hoành \( \Leftrightarrow 2ab = 0 \Leftrightarrow \left[ \begin{array}{l}a = 0\\b = 0\end{array} \right..\)
Với \(a = 0 \Rightarrow z = bi\) \( \Rightarrow \) Điểm biểu diễn nằm trên trục tung
Với \(b = 0 = > z = a\) \( \Rightarrow \) Điểm biểu diễn nằm trên trục hoành.
Vậy tập hợp tất cả các điểm biểu diễn của z nằm trên trục tung và trục hoành.
Điểm nào trong hình vẽ bên là điểm biểu diễn số phức \(z = - 1 + 2i\) ?
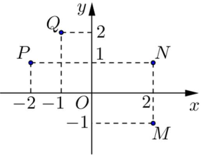
Điểm biểu diễn số phức \(z = - 1 + 2i\) là \(Q\left( { - 1;2} \right)\)
Đề thi THPT QG – 2021 lần 1– mã 104
Trên mặt phẳng tọa độ, điểm \(M\left( { - 4;3} \right)\) là điểm biểu diễn của số phức nào dưới đây?
Ta có: điểm \(M\left( { - 4;3} \right)\) là điểm biểu diễn của số phức \({z_1} = - 4 + 3i\).
Trên mặt phẳng tọa độ Oxy, gọi M , N , P theo thứ tự là các điểm biểu diễn các số phức \({z_1} = 3 - 2i,\)\({z_2} = 5 - 10i,\,{z_3} = 10 + 3i\). Tọa độ trọng tâm của tam giác MNP là
Ta có: \(\left\{ \begin{array}{l}{z_1} = 3 - 2i\\{z_2} = 5 - 10i\\{z_3} = 10 + 3i\end{array} \right. \Rightarrow \left\{ \begin{array}{l}M\left( {3;\, - 2} \right)\\N\left( {5;\, - 10} \right)\\P\left( {10;\,\,3} \right)\end{array} \right.\)
Gọi \(G\left( {{x_G};\,{y_G}} \right)\) là trọng tâm \(\Delta MNP\) \( \Rightarrow \left\{ \begin{array}{l}{x_G} = \dfrac{{3 + 5 + 10}}{3} = 6\\{y_G} = \dfrac{{ - 2 - 10 + 3}}{3} = - 3\end{array} \right.\) \( \Rightarrow G\left( {6; - 3} \right).\)
Gọi \({z_1}\) là nghiệm phức có phần ảo âm của phương trình \({z^2} - 2z + 5 = 0\). Hỏi điểm biểu diễn của \(w = (1 + i){z_1}\) là điểm nào trong các điểm trong các điểm M, N, P, Q ở hình bên?
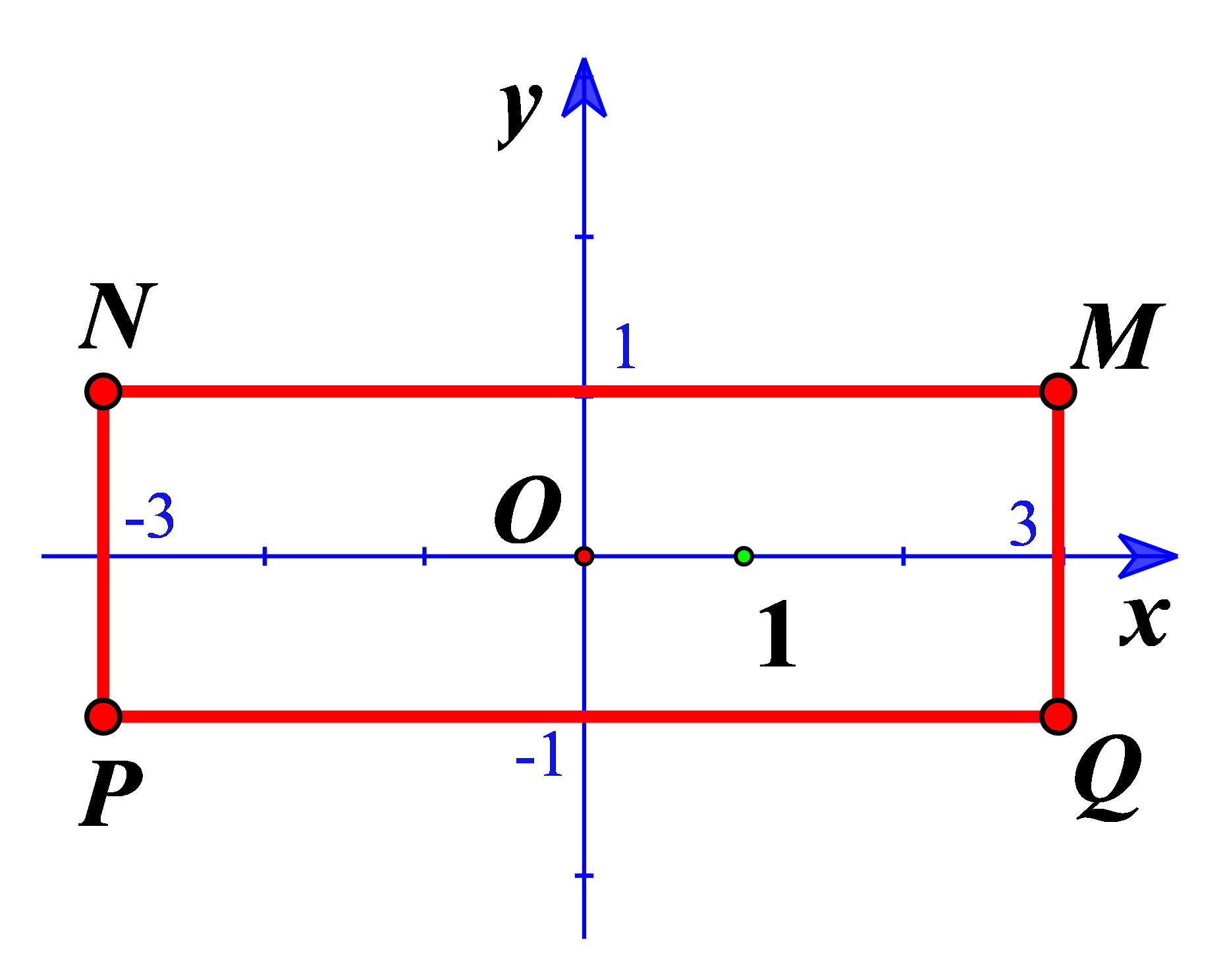
Bước 1: Tìm nghiệm của phương trình.
Ta có \({z^2} - 2z + 5 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{z_1} = 1 - 2i}\\{{z_2} = 1 + 2i}\end{array}} \right.\).
Bước 2: Tìm điểm biểu diễn số phức w.
Suy ra \(w = (1 + i){z_1} = (1 + i)(1 - 2i) = 3 - i\).
Vậy tọa độ điểm biểu diễn số phức \(w = (1 + i){z_1}\) là điểm \(Q(3; - 1)\).
Đề thi THPT QG - 2021 - mã 101
Trên mặt phẳng tọa độ, điểm \(M\left( { - 3;4} \right)\) là điểm biểu diễn của số phức nào dưới đây?
Điểm \(M\left( { - 3;4} \right)\) là điểm biểu diễn của số phức \({z_3} = - 3 + 4i\).
Trong mặt phẳng tọa độ \(Oxy,\) cho số phức \(z = - 4 - 5i,\) điểm biểu diễn số phức \(\overline z \) có tọa độ là:
Ta có: \(z = - 4 - 5i \Rightarrow \overline z = - 4 + 5i\)
\( \Rightarrow M\left( { - 4;\,\,5} \right)\) là điểm biểu diễn số phức \(\overline z .\)
Cho số phức \(z = 2 - 3i.\) Trên mặt phẳng tọa độ, điểm biểu diễn số phức \({\rm{w}} = \overline z .i\) là điểm nào dưới đây?
Ta có: \(z = 2 - 3i \Rightarrow \overline z = 2 + 3i\)
\( \Rightarrow {\rm{w}} = \overline z i = \left( {2 + 3i} \right)i = 2i + 3{i^2} = - 3 + 2i.\)
\( \Rightarrow \) Số phức \(w\) có điểm biểu diễn là \(A\left( { - 3;\,\,2} \right).\)
Biết rằng tập hợp điểm biểu diễn các số phức \(z\) thỏa mãn \(\left| {\left( {1 - 2i} \right)z + 4 + i} \right| = 1\) là đường tròn tâm \(I\left( {a;b} \right)\). Tính \(a + b\).
Điền số nguyên hoặc phân số dạng a/b
Đáp án:
Đáp án:
Ta có \(\left| {\left( {1 - 2i} \right)z + 4 + i} \right| = 1\) (1)
Đặt \(z = x + yi,\,\,x,y \in \mathbb{R}\).
Phương trình (1) tương đương với: \(\left| {\left( {1 - 2i} \right)\left( {x + yi} \right) + 4 + i} \right| = 1\)
\( \Leftrightarrow \left| {x + yi - 2xi + 2y + 4 + i} \right| = 1\)
\( \Leftrightarrow \left| {x + 2y + 4 + \left( {y - 2x + 1} \right)i} \right| = 1\)
\( \Leftrightarrow \sqrt {{{\left( {x + 2y + 4} \right)}^2} + {{\left( {y - 2x + 1} \right)}^2}} = 1\)
\( \Leftrightarrow {\left( {x + 2y} \right)^2} + 8\left( {x + 2y} \right) + 16 + {\left( {y - 2x} \right)^2} + 2\left( {y - 2x} \right) + 1 = 1\)
\( \Leftrightarrow {x^2} + 4xy + 4{y^2} + 8x + 16y + 16 + {y^2} - 4xy + 4{x^2} + 2y - 4x = 0\)
\( \Leftrightarrow 5{x^2} + 5{y^2} + 4x + 18y + 16 = 0\)
\( \Leftrightarrow {x^2} + {y^2} + \dfrac{4}{5}x + \dfrac{{18}}{5}y + \dfrac{{16}}{5} = 0\).
Suy ra tập hợp các điểm biểu diễn số phức \(z\) là đường tròn tâm \(I\left( { - \dfrac{2}{5}; - \dfrac{9}{5}} \right)\).
Tức là, \(a = - \dfrac{2}{5},\,\,b = - \dfrac{9}{5}\).
\( \Rightarrow a + b = - \dfrac{2}{5} - \dfrac{9}{5} = - \dfrac{{11}}{5}\).
Vậy \(a + b = - \dfrac{{11}}{5}\).
Xét các số phức z thỏa mãn \(\left( {z + 2i} \right)\left( {\overline z + 2} \right)\) là số thuần ảo. Biết rằng tập hợp tất cả các điểm biểu diễn của z là một đường tròn, tâm của đường tròn đó có tọa độ là:
Đặt \(z = a + bi\;\;\left( {a,\;b \in R} \right)\)
\(\begin{array}{l} \Rightarrow \left( {z + 2i} \right)\left( {\overline z + 2} \right) = \left[ {a + \left( {b + 2} \right)i} \right]\left( {a + 2 - bi} \right)\\ = a\left( {a + 2} \right) + b\left( {b + 2} \right) + \left[ {\left( {a + 2} \right)\left( {b + 2} \right) - ab} \right]i\end{array}\)
Số \(\left( {z + 2i} \right)\left( {\overline z + 2} \right)\) là số thuần ảo \( \Leftrightarrow \) Phần thực \( = 0 \Leftrightarrow {a^2} + 2a + {b^2} + 2b = 0 \Leftrightarrow {\left( {a + 1} \right)^2} + {\left( {b + 1} \right)^2} = 2\)
Vậy đường tròn tâm biểu diễn số phức đã cho có tâm là \(I\left( { - 1; - 1} \right)\)
Cho số phức \(z = - 2 + i.\) Trong hình bên điểm biểu diễn số phức \(\overline z \) là:
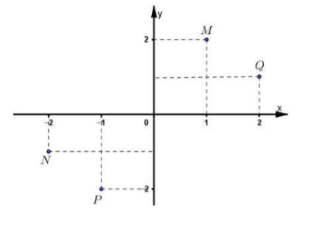
Ta có: \(z = - 2 + i \Rightarrow \overline z = - 2 - i \Rightarrow N\left( { - 2; - 1} \right)\) là điểm biểu diễn số phức \(\overline z .\)
Cho số phức \(z = 2 + 3i\) có điểm biểu diễn trên mặt phẳng tọa độ là:
Điểm biểu diễn của số phức \(z = 2 + 3i\) là: \(\left( {2;\,\,3} \right).\)
Cho số phức \(z\) thỏa mãn \(z + 2\overline z = 6 + 2i.\) Điểm biểu diễn số phức \(z\) có tọa độ là:
Gọi số phức \(z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right) \Rightarrow \overline z = a - bi.\) Khi đó ta có:
\(\begin{array}{l}\,\,\,\,\,\,z + 2\overline z = 6 + 2i \Leftrightarrow a + bi + 2\left( {a - bi} \right) = 6 + 2i\\ \Leftrightarrow 3a - bi = 6 + 2i \Leftrightarrow \left\{ \begin{array}{l}3a = 6\\ - b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = - 2\end{array} \right. \Rightarrow z = 2 - 2i\end{array}\)
\( \Rightarrow M\left( {2; - 2} \right)\) là điểm biểu diễn số phức \(z.\)
Điểm nào trong hình vẽ dưới đây là biểu diễn hình học của số phức \(z = \left( { - 1 - 2i} \right)\left( {3 + i} \right) - 2 + 6i?\)

Ta có : \(z = \left( { - 1 - 2i} \right)\left( {3 + i} \right) - 2 + 6i\) \( = - 3 - 6i - i - 2{i^2} - 2 + 6i = - 3 - i\).
Do đó \(z = - 3 - i \Rightarrow P\left( { - 3; - 1} \right)\) biểu diễn số phức \(z\).
Đề thi THPT QG - 2021 - mã 102
Trên mặt phẳng tọa độ, điểm \(M\left( { - 3;2} \right)\) là điểm biểu diễn của số phức nào dưới đây?
Ta có điểm \(M\left( { - 3;2} \right)\) là điểm biểu diễn của số phức \({z_2} = - 3 + 2i\)
Cho hai số phức \({z_1} = 2 + 3i\) và \({z_2} = 3 - 2i.\) Tọa độ điểm biểu diễn số phức \({z_1} - {z_2}\) là:
Ta có: \(\left\{ \begin{array}{l}{z_1} = 2 + 3i\\{z_2} = 3 - 2i\end{array} \right.\) \( \Rightarrow {z_1} - {z_2} = \left( {2 - 3} \right) + \left( {3 + 2} \right)i = - 1 + 5i\)
\( \Rightarrow M\left( { - 1;\,\,5} \right)\) là điểm điểm biểu diễn số phức \({z_1} - {z_2}.\)

