Có bao nhiêu số phức \(z\) thỏa mãn đồng thời hai điều kiện: \(\left| z \right| = 2\) và \({z^2}\) là số thuần ảo?
Gọi số phức \(z = x + yi\,\left( {x;y \in \mathbb{R}} \right)\) có mô đun \(\left| z \right| = \sqrt {{x^2} + {y^2}} \)
Từ đề bài ta có \(\left| z \right| = 2 \Leftrightarrow {x^2} + {y^2} = 4\)
Và \({z^2} = {\left( {x + yi} \right)^2} = {x^2} - {y^2} + 2xyi\) là số thuần ảo \( \Leftrightarrow {x^2} - {y^2} = 0 \Leftrightarrow \left[ \begin{array}{l}x = y\\x = - y\end{array} \right.\)
+ Với \(x = y \Rightarrow {x^2} + {y^2} = 4 \Leftrightarrow 2{x^2} = 4 \Leftrightarrow \left[ \begin{array}{l}x = \sqrt 2 \Rightarrow y = \sqrt 2 \\x = - \sqrt 2 \Rightarrow y = - \sqrt 2 \end{array} \right.\)
+ Với \(x = - y \Rightarrow {x^2} + {y^2} = 4 \Leftrightarrow 2{x^2} = 4 \Leftrightarrow \left[ \begin{array}{l}x = \sqrt 2 \Rightarrow y = - \sqrt 2 \\x = - \sqrt 2 \Rightarrow y = - \sqrt 2 \end{array} \right.\)
Vậy có 4 số phức thỏa mãn đề bài \(\sqrt 2 + \sqrt 2 i;\, - \sqrt 2 - \sqrt 2 i;\,\sqrt 2 - \sqrt 2 i;\, - \sqrt 2 + \sqrt 2 i\)
Cho hai số phức \({z_1},{z_2}\) thoả mãn \(\left| {{z_1}} \right| = 2,\left| {{z_2}} \right| = \sqrt 3 \). Gọi M, N là các điểm biểu diễn cho \({z_1}\) và \(i{z_2}\). Biết \(\widehat {MON} = {30^0}\). Tính \(S = \left| {z_1^2 + 4z_2^2} \right|\).
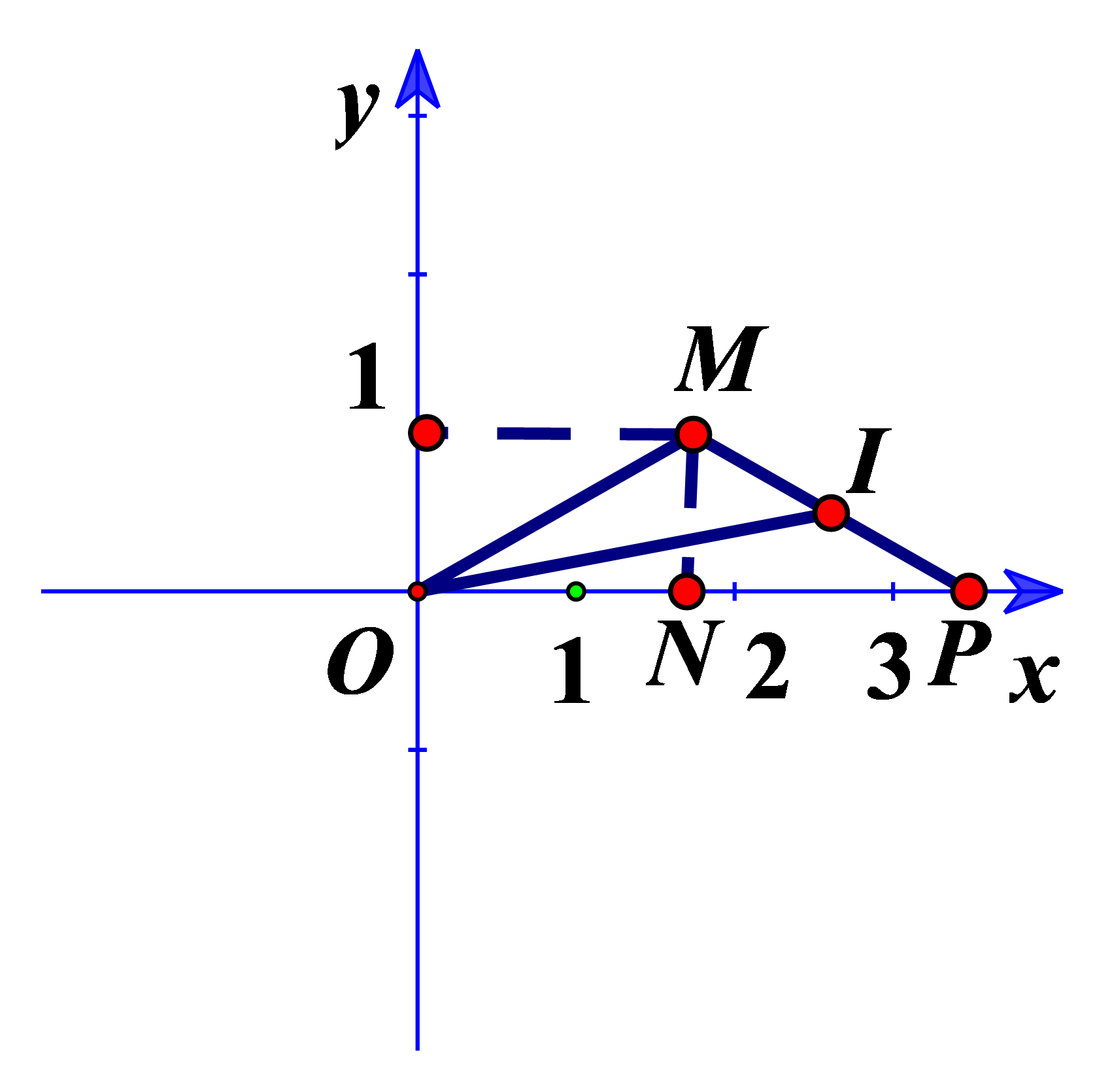
Bước 1: Phân tích \(S = \left| {{z_1} - 2i{z_2}} \right|.\left| {{z_1} + 2i{z_2}} \right|\)
Ta có \(S = \left| {z_1^2 + 4z_2^2} \right| = \left| {z_1^2 - {{\left( {2i{z_2}} \right)}^2}} \right|\)\( = \left| {{z_1} - 2i{z_2}} \right|.\left| {{z_1} + 2i{z_2}} \right|\)
Bước 2: Gọi \(P\) là điểm biểu diễn của số phức \(2i{z_2}\). Chứng minh \(\left| {{z_1} - 2i{z_2}} \right|.\left| {{z_1} + 2i{z_2}} \right| = 2PM.OI\)
Gọi \(P\) là điểm biểu diễn của số phức \(2i{z_2}\).
Khi đó, ta có \(\left| {{z_1} - 2i{z_2}} \right| \cdot \left| {{z_1} + 2i{z_2}} \right| = |\overrightarrow {OM} - \overrightarrow {OP} | \cdot |\overrightarrow {OM} + \overrightarrow {OP} |\)
\(\left| {{z_1} - 2i{z_2}} \right| \cdot \left| {{z_1} + 2i{z_2}} \right| = \left| {\overrightarrow {PM} } \right| \cdot \left| {2\overrightarrow {OI} } \right| = 2PM.OI\) (I là trung điểm PM).
Bước 3: Tính S.
Do \(\widehat {MON} = {30^0}\) nên áp dụng định lí cosin ta tính được \(MN = 1\).
Khi đó \(\Delta OMP\) có MN đồng thời là đường cao và đường trung tuyến, suy ra \(\Delta OMP\) cân tại \(M \Rightarrow PM = OM = 2\). suy ra \(\Delta OMP\) cân tại \(M \Rightarrow PM = OM = 2.\)
Áp dụng định lí đường trung tuyến cho \(\Delta OMN\) ta có: \(O{I^2} = \dfrac{{O{M^2} + O{P^2}}}{2} - \dfrac{{M{P^2}}}{4} = 7\). Vầy \(S = 2PM.OI = 2 \cdot 2 \cdot \sqrt 7 = 4\sqrt 7 \).
Trong mặt phẳng tọa độ Oxy, số phức \(z = 2i\) được biểu diễn bởi điểm nào sau đây?
Số phức \(z = 2i\) có điểm biểu diễn trên mặt phẳng phức là \(P\left( {0;2} \right)\).
Có bao nhiêu số phức z thỏa mãn \({\left| z \right|^2} = 2\left| {z + \overline z } \right| + 4\) và \(\left| {z - 1 - i} \right| = \left| {z - 3 + 3i} \right|\) ?
Gọi số phức \(z = a + bi \Rightarrow \overline z = a - bi\).
Từ giả thiết thứ nhất ta có:
\({\left| z \right|^2} = 2\left| {z + \overline z } \right| + 4 \Leftrightarrow {a^2} + {b^2} = 2\left| {a + bi + a - bi} \right| + 4 \Leftrightarrow {a^2} + {b^2} - 2.2\left| a \right| - 4 = 0 \Leftrightarrow \left[ \begin{array}{l}{a^2} + {b^2} - 4a - 4 = 0\\{a^2} + {b^2} + 4a - 4 = 0\end{array} \right.\)
\( \Rightarrow \) Tập hợp các số phức z là đường tròn \(\left( {{C_1}} \right):\,\,{x^2} + {y^2} - 4x - 4 = 0\) hoặc \(\left( {{C_2}} \right):\,\,{x^2} + {y^2} + 4x - 4 = 0\).
Từ giả thiết thứ hai ta có:
\(\begin{array}{l}\;\;\;\;\left| {z - 1 - i} \right| = \left| {z - 3 + 3i} \right|\\ \Leftrightarrow \left| {a - 1 + bi - i} \right| = \left| {a - 3 + bi + 3i} \right|\\ \Leftrightarrow {\left( {a - 1} \right)^2} + {\left( {b - 1} \right)^2} = {\left( {a - 3} \right)^2} + {\left( {b + 3} \right)^2}\\ \Leftrightarrow - 2a + 1 - 2b + 1 = - 6a + 9 + 6b + 9\\ \Leftrightarrow 4a - 8b - 16 = 0\\ \Leftrightarrow a - 2b - 4 = 0\end{array}\)
\( \Rightarrow \) Tập hợp các số phức z là đường thẳng \(x - 2y - 4 = 0\,\,\left( d \right)\).
Vậy số phức thỏa mãn 2 giả thiết trên là số giao điểm của \(d\) với \(\left( {{C_1}} \right)\) và \(\left( d \right)\) với \(\left( {{C_2}} \right)\).
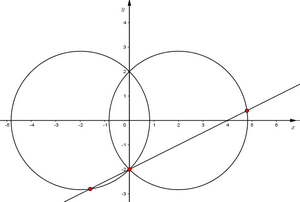
Dựa vào hình vẽ ta thấy có 3 giao điểm của \(d\) với \(\left( {{C_1}} \right)\) và \(\left( d \right)\) với \(\left( {{C_2}} \right)\). Vậy có 3 số phức thỏa mãn yêu cầu bài toán.
Số phức nào sau đây có biểu diễn hình học là điểm \(M\left( {3; - 5} \right).\)
Điểm \(M\left( {3; - 5} \right)\) là điểm biểu diễn hình học của số phức \(z = 3 - 5i.\)
Trong mặt phẳng tọa độ, tập hợp điểm \(M\left( {x;y} \right)\) biểu diễn của số phức \(z = x + yi,\,\,\left( {x,y \in \mathbb{R}} \right)\) thỏa mãn \(\left| {z - 1 + 3i} \right| = \left| {z - 2 - i} \right|\) là:
Ta có: \(\left| {z - 1 + 3i} \right| = \left| {z - 2 - i} \right| \Leftrightarrow \sqrt {{{\left( {x - 1} \right)}^2} + {{\left( {y + 3} \right)}^2}} = \sqrt {{{\left( {x - 2} \right)}^2} + {{\left( {y - 1} \right)}^2}} \)
\( \Rightarrow \) Tập hợp điểm \(M\left( {x;y} \right)\) biểu diễn của số phức \(z = x + yi,\,\,\left( {x,y \in \mathbb{R}} \right)\) là đường thẳng trung trực của đoạn thẳng $AB$ với \(A\left( {1; - 3} \right),\,B\left( {2;1} \right)\).
Cho \(z = 25i - 3.\) Trên mặt phẳng tọa độ, điểm biểu diễn số phức \(\overline z \) là điểm nào dưới đây?
Ta có: \(z = 25i - 3 = - 3 + 25i\) \( \Rightarrow \overline z = - 3 - 25i\)
\( \Rightarrow Q\left( { - 3; - 25} \right)\) là điểm biểu diễn số phức \(\overline z .\)
Xét các số phức \(z\) thỏa mãn \(\left| z \right| = 2\sqrt 2 \). Biết rằng tập hợp tất cả các điểm biểu diễn của số phức \(w = \dfrac{{z + 1 - i}}{{iz + 3}}\) là một đường tròn, bán kính của đường tròn đó bằng
Ta có : \(w = \dfrac{{z + 1 - i}}{{iz + 3}} \Leftrightarrow z + 1 - i = wiz + 3w \Leftrightarrow z\left( {1 - iw} \right) = 3w + i - 1 \Leftrightarrow z = \dfrac{{3w + i - 1}}{{1 - iw}}\)
Đặt \(w = a + bi\left( {a,b \in \mathbb{R}} \right)\) thì \(z = \dfrac{{3\left( {a + bi} \right) + i - 1}}{{1 - i\left( {a + bi} \right)}} = \dfrac{{3a - 1 + \left( {3b + 1} \right)i}}{{1 + b - ai}}\)
Mà
\(\begin{array}{l}\left| z \right| = 2\sqrt 2 \Rightarrow \left| {\dfrac{{3a - 1 + \left( {3b + 1} \right)i}}{{1 + b - ai}}} \right| = 2\sqrt 2 \Leftrightarrow \dfrac{{\left| {3a - 1 + \left( {3b + 1} \right)i} \right|}}{{\left| {1 + b - ai} \right|}} = 2\sqrt 2 \\ \Leftrightarrow \sqrt {{{\left( {3a - 1} \right)}^2} + {{\left( {3b + 1} \right)}^2}} = \sqrt {\left( {1 + {b^2}} \right) + {a^2}} .2\sqrt 2 \\ \Leftrightarrow 9{a^2} - 6a + 1 + 9{b^2} + 6b + 1 = 8\left( {{a^2} + {b^2} + 2b + 1} \right)\\ \Leftrightarrow {a^2} + {b^2} - 6a - 10b - 6 = 0 \Leftrightarrow {\left( {a - 3} \right)^2} + {\left( {b - 5} \right)^2} = 40\end{array}\)
Suy ra tập hợp điểm biểu diễn số phức \(w\) là đường tròn tâm \(I\left( {3;5} \right)\) bán kính \(R = 2\sqrt {10} \).
Trong mặt phẳng tọa độ Oxy, gọi M, N, P lần lượt là các điểm biểu diễn các số phức \({z_1} = 1 + i,{z_2} = 8 + i,{z_3} = 1 - 3i\). Khẳng định nào sau đây đúng?
Vì \(M\) là điểm biểu diễn số phức \({z_1} = 1 + i\) nên tọa độ điểm \(M\) là \((1;1)\).
Vì \(N\) là điểm biểu diễn số phức \({z_2} = 8 + i\) nên tọa độ điểm \(N\) là \((8;1)\).
Vì \(P\) là điểm biểu diễn số phức \({z_3} = 1 - 3i\) nên tọa độ điểm \(P\) là \((1; - 3)\).
Ta có \(\overrightarrow {MN} = (7;0),\overrightarrow {MP} = (0; - 4)\) nên \(\left\{ {\begin{array}{*{20}{l}}{\overrightarrow {MN} \cdot \overrightarrow {MP} = 0}\\{|\overrightarrow {MN} | \ne |\overrightarrow {MP} |}\end{array}} \right.\) hay tam giác MNP vuông tại \(M\) và không phải tam giác cân.
Gọi \(A,B\) lần lượt là điểm biểu diễn cho hai số phức \({z_1} = 1 + i\) và \({z_2} = 1 - 3i.\) Gọi M là trung điểm của AB. Khi đó M là điểm biểu diễn cho số phức nào dưới đây ?
Do \(A,\,\,B\) lần lượt là điểm biểu diễn cho hai số phức \({z_1} = 1 + i\) và \({z_2} = 1 - 3i\) \( \Rightarrow A\left( {1;1} \right),\,B\left( {1; - 3} \right)\).
Vì \(M\) là trung điểm của \(AB\) \( \Rightarrow M\left( {1; - 1} \right) \Rightarrow \)
Vậy điểm \(M\left( {1; - 1} \right)\) là điểm biểu diễn cho số phức \(1 - i.\)
Trong mặt phẳng tọa độ \(Oxy\), gọi \(A,B,C\) lần lượt là các điểm biểu diễn các số phức \({z_1},{z_2}\) , \({z_1} + {z_2}\). Xét các mệnh đề sau:
1) \(\left| {{z_1}} \right| = \left| {{z_2}} \right| \Leftrightarrow \left[ \begin{array}{l}{z_1} = {z_2}\\{z_1} = - {z_2}\end{array} \right.\).
2) \(\left| {{z_1} + {z_2}} \right| \le \left| {{z_1}} \right| + \left| {{z_2}} \right|\).
3) Nếu \(\overrightarrow {OA} .\overrightarrow {OB} = 0\) thì \({z_1}.\overline {{z_2}} + {z_2}.\overline {{z_1}} = 0\).
4) \(O{C^2} + A{B^2} = 2\left( {O{A^2} + O{B^2}} \right)\).
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng?
1) \(\left| {{z_1}} \right| = \left| {{z_2}} \right| \Leftrightarrow \left[ \begin{array}{l}{z_1} = {z_2}\\{z_1} = - {z_2}\end{array} \right.\): Sai
2) \(\left| {{z_1} + {z_2}} \right| \le \left| {{z_1}} \right| + \left| {{z_2}} \right|\): Đúng
3) Nếu \(\overrightarrow {OA} .\overrightarrow {OB} = 0\) thì \({z_1}.\overline {{z_2}} + {z_2}.\overline {{z_1}} = 0\): Đúng
Giả sử \({z_1} = {a_1} + {b_1}i,\,\,\,{z_2} = {a_2} + {b_2}i,\,\,A\left( {{a_1};{b_1}} \right),\,\,B\left( {{a_2};{b_2}} \right)\). Khi đó:
\(\overrightarrow {OA} .\overrightarrow {OB} = 0 \Leftrightarrow {a_1}.{a_2} + {b_1}{b_2} = 0 \Leftrightarrow \left( {{a_1} + {b_1}i} \right).\left( {{a_2} - {b_2}i} \right) + \left( {{a_1} - {b_1}i} \right).\left( {{a_2} + {b_2}i} \right) = 0 \Leftrightarrow \)\({z_1}.\overline {{z_2}} + {z_2}.\overline {{z_1}} = 0\).
4) \(O{C^2} + A{B^2} = 2\left( {O{A^2} + O{B^2}} \right)\): Đúng
Giả sử \({z_1} = {a_1} + {b_1}i,\,\,\,{z_2} = {a_2} + {b_2}i,\,\,A\left( {{a_1};{b_1}} \right),\,\,B\left( {{a_2};{b_2}} \right),\,\,C\left( {{a_1} + {a_2};{b_1} + {b_2}} \right)\). Khi đó:
\(O{C^2} + A{B^2} = {\left( {{a_1} + {a_2}} \right)^2} + {\left( {{b_1} + {b_2}} \right)^2} + {\left( {{a_1} - {a_2}} \right)^2} + {\left( {{b_1} - {b_2}} \right)^2} = 2{a_1}^2 + 2{b_1}^2 + 2{a_2}^2 + 2{b_2}^2 = 2\left( {O{A^2} + O{B^2}} \right)\).
Trên mặt phẳng tọa độ ,điểm \(M\) trong hình vẽ bên là điểm biểu diễn số phức \(z\). Khẳng định nào sau đây là đúng?
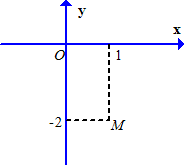
Ta có \(M\left( {1; - 2} \right)\) là điểm biểu phức z nên \(z = 1 - 2i\)
\(\begin{array}{l} \Rightarrow \overline z = 1 + 2i\\\,\,\,\,\,\left| z \right| = \sqrt {{1^2} + {{\left( { - 2} \right)}^2}} = \sqrt 5 .\end{array}\)
Vậy khẳng định B đúng.
Tìm tập hợp các điểm biểu diễn số phức \(z\) thỏa mãn \(\left| {z - 1 + 3i} \right| = \left| {\overline z + 1 - i} \right|\).
Theo bài ra ta có
\(\begin{array}{l}\,\,\,\,\,\,\,\left| {z - 1 + 3i} \right| = \left| {\overline z + 1 - i} \right|\\ \Leftrightarrow \left| {z - 1 + 3i} \right| = \left| {\overline z + \overline {1 + i} } \right|\\ \Leftrightarrow \left| {z - 1 + 3i} \right| = \left| {\overline {z + 1 + i} } \right|\\ \Leftrightarrow \left| {z - 1 + 3i} \right| = \left| {z + 1 + i} \right|\end{array}\)
Đặt \(z = a + bi\) ta có:
\(\begin{array}{l}\left| {a + bi - 1 + 3i} \right| = \left| {a + bi + 1 + i} \right|\\ \Leftrightarrow \left| {\left( {a - 1} \right) + \left( {b + 3} \right)i} \right| = \left| {a + 1 + \left( {b + 1} \right)i} \right|\\ \Leftrightarrow {\left( {a - 1} \right)^2} + {\left( {b + 3} \right)^2} = {\left( {a + 1} \right)^2} + {\left( {b + 1} \right)^2}\\ \Leftrightarrow - 2a + 1 + 6b + 9 = 2a + 1 + 2b + 1\\ \Leftrightarrow 4a - 4b - 8 = 0\\ \Leftrightarrow a - b - 2 = 0\end{array}\)
Vậy tập hợp các điểm biểu diễn số phức \(z\) là đường thẳng \(x - y - 2 = 0\).
Trong mặt phẳng tọa độ Oxy cho các điểm A, B như hình vẽ bên.
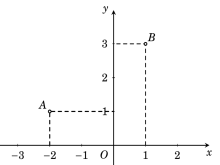
Trung điểm của đoạn thẳng AB biểu diễn số phức
Dựa vào hình vẽ ta thấy \(A\left( { - 2;1} \right),\,\,B\left( {1;3} \right)\).
Gọi I là trung điểm của AB \( \Rightarrow I\left( { - \dfrac{1}{2};2} \right)\).
Vậy trung điểm của đoạn thẳng AB biểu diễn số phức \( - \dfrac{1}{2} + 2i\).
Đề thi THPT QG 2020 – mã đề 104
Trên mặt phẳng tọa độ, biết \(M\left( { - 1;\,\,2} \right)\)là điểm biểu diễn của số phức z. Phần thực của z bằng
Điểm \(M\left( { - 1;\,\,2} \right)\) là điểm biểu diễn số phức \(z\) \( \Rightarrow z = - 1 + i.\)
\( \Rightarrow \) Phần thực của số phức \(z\) là \( - 1\).
Trong mặt phẳng phức, cho ba điểm \(A,\,\,B,\,\,C\) lần lượt biểu diễn ba số phức \({z_1} = 1 + i\), \({z_2} = {\left( {1 + i} \right)^2}\) và \({z_3} = a - i\). Để tam giác ABC vuông tại B thì a bằng:
Vì A, B, C lần lượt là các điểm biểu diễn ba số phức \({z_1} = 1 + i\), \({z_2} = {\left( {1 + i} \right)^2} = 2i\) và \({z_3} = a - i\) nên ta có A(1;1), B(0;2) và C(a;-1).
Ta có: \(\overrightarrow {BA} = \left( {1; - 1} \right),\,\,\overrightarrow {BC} = \left( {a; - 3} \right)\).
Tam giác ABC vuông tại B thì \(\overrightarrow {BA} .\overrightarrow {BC} = 0\).
\( \Leftrightarrow 1.a - 1.\left( { - 3} \right) = 0 \Leftrightarrow a + 3 = 0 \Leftrightarrow a = - 3\)
Cho số phức \(z = m - 2 + \left( {{m^2} - 1} \right)i,m \in \mathbb{R}\). Gọi \(\left( C \right)\) là tập hợp các điểm biểu diễn số phức z trong mặt phẳng tọa độ. Diện tích hình phẳng giới hạn bởi \(\left( C \right)\) và trục hoành bằng
Ta có điểm biểu diễn của số phức z là \(M\left( {m - 2;{m^2} - 1} \right) \Rightarrow \left\{ \begin{array}{l}x = m - 2\\y = {m^2} - 1\end{array} \right.\)
\( \Rightarrow y + 1 = {\left( {x + 2} \right)^2} \Leftrightarrow y = {x^2} + 4x + 3\)
\( \Rightarrow \left( C \right):\,\,y = {x^2} + 4x + 3\) là 1 parabol.
Hoành độ giao điểm của đồ thị hàm số \(y = {x^2} + 4x + 3\) với trục hoành là: \({x^2} + 4x + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = - 1\end{array} \right.\)
Diện tích hình phẳng cần tìm là \(S = \int\limits_{ - 3}^{ - 1} {\left| {{x^2} + 4x + 3} \right|dx} = - \int\limits_{ - 3}^{ - 1} {\left( {{x^2} + 4x + 3} \right)} = \dfrac{4}{3}.\)
Biết rằng \(z\) là số phức có môđun nhỏ nhất thỏa mãn \(\left( {1 - z} \right)\left( {\bar z + 2i} \right)\) là số thực. Số phức \(z\) là:
Cách 1:
Gọi \(z = x + yi\,\,\left( {x,\,\,y \in \mathbb{R}} \right)\), theo bài ra ta có:
\(\begin{array}{l}\,\,\,\,\left( {1 - z} \right)\left( {\bar z + 2i} \right)\\ = \left( {1 - x - yi} \right)\left( {x - yi + 2i} \right)\\ = \left( {1 - x - yi} \right)\left( {x - \left( {y - 2} \right)i} \right)\\ = \left( {1 - x} \right)x - \left( {1 - x} \right)\left( {y - 2} \right)i - xyi - y\left( {y - 2} \right)\\ = \left[ {\left( {1 - x} \right)x - y\left( {y - 2} \right)} \right] - \left[ {\left( {1 - x} \right)\left( {y - 2} \right) + xy} \right]i\end{array}\)
Để \(\left( {1 - z} \right)\left( {\bar z + 2i} \right)\) là số thực thì \({\mathop{\rm Im}\nolimits} \left( {1 - z} \right)\left( {\bar z + 2i} \right) = 0\)
\(\begin{array}{l} \Leftrightarrow \left( {1 - x} \right)\left( {y - 2} \right) + xy = 0\\ \Leftrightarrow y - 2 - xy + 2x + xy = 0\\ \Leftrightarrow y = 2 - 2x\end{array}\)
Khi đó ta có: \({\left| z \right|^2} = {x^2} + {y^2} = {x^2} + {\left( {2 - 2x} \right)^2} = 5{x^2} - 8x + 4\).
\( \Rightarrow {\left| z \right|_{\min }} \Leftrightarrow {\left| z \right|^2}_{\min } \Leftrightarrow x = \dfrac{8}{{2.5}} = \dfrac{4}{5}\), khi đó \(y = 2 - 2.\dfrac{4}{5} = \dfrac{2}{5}\).
Vậy số phức \(z\) thỏa mãn yêu cầu bài toán là: .\(z = \dfrac{4}{5} + \dfrac{2}{5}i\).
Cho số phức $z$ thỏa mãn $\left( {2-i} \right)z = 7-i$ . Hỏi điểm biểu diễn của $z$ là điểm nào trong các điểm $M,N,P,Q$ ở hình dưới.
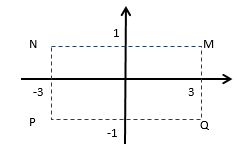
\(\left( {2 - i} \right)z = 7 - i \Rightarrow z = \dfrac{{7 - i}}{{2 - i}} = \dfrac{{(7 - i)(2 + i)}}{5} = \dfrac{{15 + 5i}}{5} = 3 + i\)
Suy ra điểm có tọa độ $\left( {3;1} \right)$ sẽ biểu diễn số phức $z$, suy ra $M$ thỏa mãn.
Trên mặt phẳng tọa độ, điểm \(M\) là điểm biểu diển của số phức \(z\) (như hình vẽ bên). Điểm nào trong hình vẽ là điểm biểu diển của số phức \(2z\)?
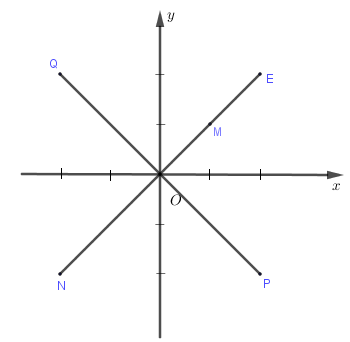
Điểm \(M\left( {1;1} \right)\) biểu diễn số phức \(z = 1 + i \Rightarrow 2z = 2 + 2i\).
Do đó điểm biểu diễn số phức \(2z\) là \(\left( {2;2} \right)\) (điểm \(E\)).

