Có bao nhiêu số phức z thỏa mãn \({\left| z \right|^2} = 2\left| {z + \overline z } \right| + 4\) và \(\left| {z - 1 - i} \right| = \left| {z - 3 + 3i} \right|\) ?
Trả lời bởi giáo viên
Gọi số phức \(z = a + bi \Rightarrow \overline z = a - bi\).
Từ giả thiết thứ nhất ta có:
\({\left| z \right|^2} = 2\left| {z + \overline z } \right| + 4 \Leftrightarrow {a^2} + {b^2} = 2\left| {a + bi + a - bi} \right| + 4 \Leftrightarrow {a^2} + {b^2} - 2.2\left| a \right| - 4 = 0 \Leftrightarrow \left[ \begin{array}{l}{a^2} + {b^2} - 4a - 4 = 0\\{a^2} + {b^2} + 4a - 4 = 0\end{array} \right.\)
\( \Rightarrow \) Tập hợp các số phức z là đường tròn \(\left( {{C_1}} \right):\,\,{x^2} + {y^2} - 4x - 4 = 0\) hoặc \(\left( {{C_2}} \right):\,\,{x^2} + {y^2} + 4x - 4 = 0\).
Từ giả thiết thứ hai ta có:
\(\begin{array}{l}\;\;\;\;\left| {z - 1 - i} \right| = \left| {z - 3 + 3i} \right|\\ \Leftrightarrow \left| {a - 1 + bi - i} \right| = \left| {a - 3 + bi + 3i} \right|\\ \Leftrightarrow {\left( {a - 1} \right)^2} + {\left( {b - 1} \right)^2} = {\left( {a - 3} \right)^2} + {\left( {b + 3} \right)^2}\\ \Leftrightarrow - 2a + 1 - 2b + 1 = - 6a + 9 + 6b + 9\\ \Leftrightarrow 4a - 8b - 16 = 0\\ \Leftrightarrow a - 2b - 4 = 0\end{array}\)
\( \Rightarrow \) Tập hợp các số phức z là đường thẳng \(x - 2y - 4 = 0\,\,\left( d \right)\).
Vậy số phức thỏa mãn 2 giả thiết trên là số giao điểm của \(d\) với \(\left( {{C_1}} \right)\) và \(\left( d \right)\) với \(\left( {{C_2}} \right)\).
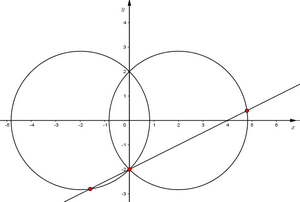
Dựa vào hình vẽ ta thấy có 3 giao điểm của \(d\) với \(\left( {{C_1}} \right)\) và \(\left( d \right)\) với \(\left( {{C_2}} \right)\). Vậy có 3 số phức thỏa mãn yêu cầu bài toán.
Hướng dẫn giải:
+) Gọi số phức \(z = a + bi \Rightarrow \overline z = a - bi\).
+) Từ mỗi giải thiết đã cho, tìm đường biểu diễn số phức z.
+) Tìm giao điểm của đường biểu diễn số phức z ở giả thiết thứ nhất và thứ 2.



