Cho hai số phức \({z_1},{z_2}\) thoả mãn \(\left| {{z_1}} \right| = 2,\left| {{z_2}} \right| = \sqrt 3 \). Gọi M, N là các điểm biểu diễn cho \({z_1}\) và \(i{z_2}\). Biết \(\widehat {MON} = {30^0}\). Tính \(S = \left| {z_1^2 + 4z_2^2} \right|\).

Bước 1: Phân tích \(S = \left| {{z_1} - 2i{z_2}} \right|.\left| {{z_1} + 2i{z_2}} \right|\)

Ta có \(S = \left| {z_1^2 + 4z_2^2} \right| = \left| {z_1^2 - {{\left( {2i{z_2}} \right)}^2}} \right|\)\( = \left| {{z_1} - 2i{z_2}} \right|.\left| {{z_1} + 2i{z_2}} \right|\)

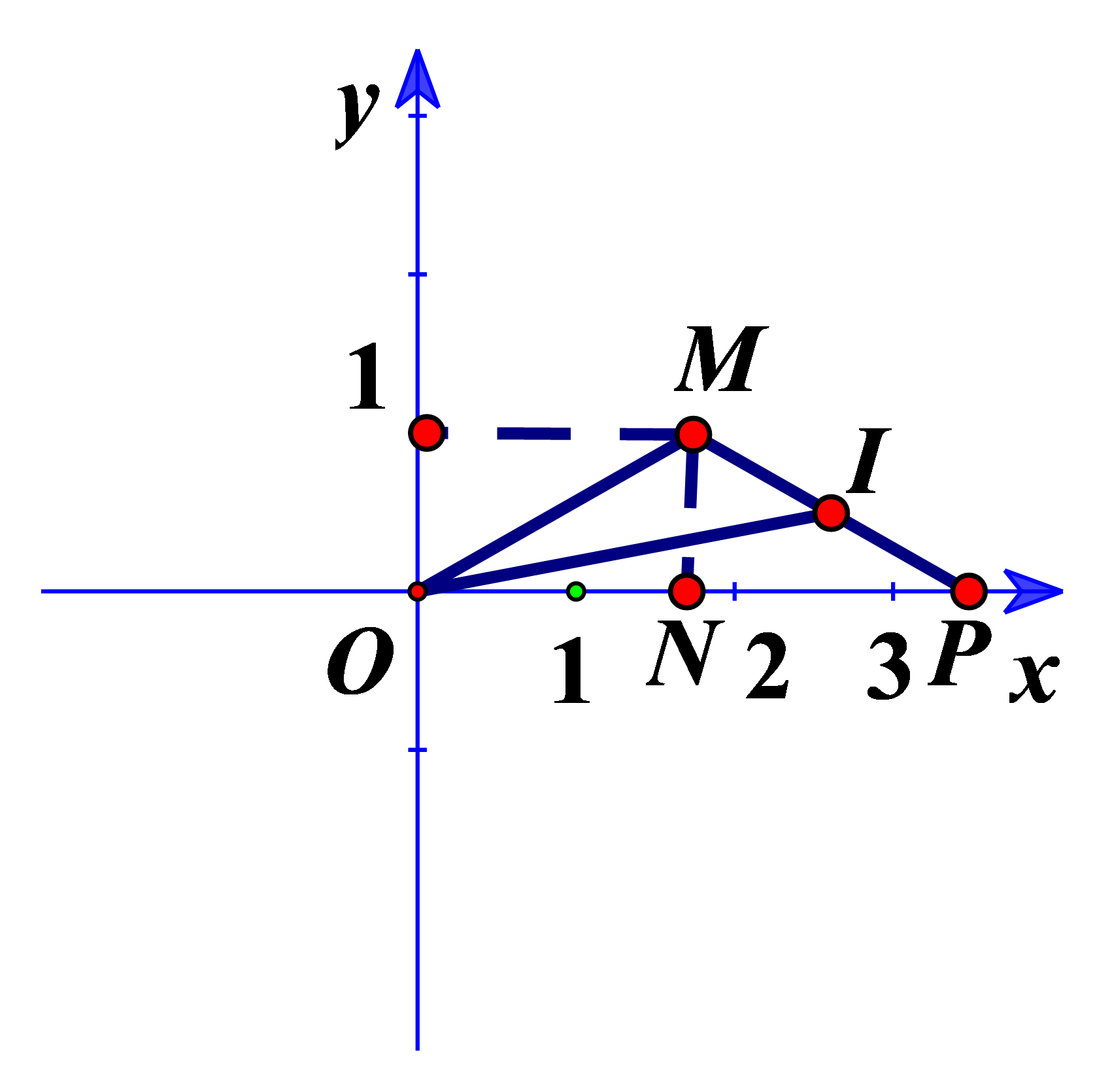
Bước 2: Gọi \(P\) là điểm biểu diễn của số phức \(2i{z_2}\). Chứng minh \(\left| {{z_1} - 2i{z_2}} \right|.\left| {{z_1} + 2i{z_2}} \right| = 2PM.OI\)

Gọi \(P\) là điểm biểu diễn của số phức \(2i{z_2}\).

Khi đó, ta có \(\left| {{z_1} - 2i{z_2}} \right| \cdot \left| {{z_1} + 2i{z_2}} \right| = |\overrightarrow {OM}  - \overrightarrow {OP} | \cdot |\overrightarrow {OM}  + \overrightarrow {OP} |\)

\(\left| {{z_1} - 2i{z_2}} \right| \cdot \left| {{z_1} + 2i{z_2}} \right| = \left| {\overrightarrow {PM} } \right| \cdot \left| {2\overrightarrow {OI} } \right| = 2PM.OI\) (I là trung điểm PM).

Bước 3: Tính S.

Do \(\widehat {MON} = {30^0}\) nên áp dụng định lí cosin ta tính được \(MN = 1\).

Khi đó \(\Delta OMP\) có MN đồng thời là đường cao và đường trung tuyến,  suy ra \(\Delta OMP\) cân tại \(M \Rightarrow PM = OM = 2\). suy ra \(\Delta OMP\) cân tại \(M \Rightarrow PM = OM = 2.\)

Áp dụng định lí đường trung tuyến cho \(\Delta OMN\) ta có: \(O{I^2} = \dfrac{{O{M^2} + O{P^2}}}{2} - \dfrac{{M{P^2}}}{4} = 7\). Vầy \(S = 2PM.OI = 2 \cdot 2 \cdot \sqrt 7  = 4\sqrt 7 \).