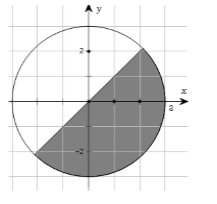
Gọi \(M\) là điểm biểu diễn của số phức \(z\), biết tập hợp các điểm \(M\) là phần tô đậm ở hình bên (kể cả biên). Mệnh đề nào sau đây đúng ?

Tìm điểm $M$ biểu diễn số phức \(z = i - 2\)

Cho số phức $z$ thỏa mãn $\left( {1 + i} \right)z = 3-i$. Hỏi điểm biểu diễn của $z$ là điểm nào trong các điểm $M,N,P,Q$ ở hình bên ?

Trên mặt phẳng tọa độ, cho hai số phức \({z_1} = 2 + i\) và \({z_2} = 1 - i.\) Điểm biểu diễn số phức \({z_1} - {z_2}\) là điểm nào dưới đây?

Trong hình bên .\(M,\,\,N\). lần lượt là điểm biểu diễn số phức \(z\) và \({\rm{w}}{\rm{.}}\) Số phức \(z + {\rm{w}}\) bằng?

Cho ba số phức \({z_1} = 4 - 3i,\) \({z_2} = \left( {1 + 2i} \right)i\) và \({z_3} = \dfrac{{1 - i}}{{1 + i}}\) có điểm biểu diễn trên mặt phẳng \(Oxy\)lần lượt là A, B, C. Số phức  nào dưới đây có điểm biểu diễn là điểm D  thỏa ABCD là hình bình hành?

Cho số phức \(z\) thỏa mãn \(\left\{ {\begin{array}{*{20}{l}}{|z - 1 - 2i| \le 1}\\{|z - 1 + 2i| \ge |z + 3 - 2i|}\end{array}.} \right.\) Gọi \(S\) là diện tích phần mặt phẳng chứa các điểm biểu diễn của số phức \(z\). Tính \(S\).

Có bao nhiêu số phức z thỏa mãn \(\left| {z + 2 - i} \right| = 2\sqrt 2 \) và \({\left( {z - i} \right)^2}\) là một số thực?