Có bao nhiêu số phức \(z = x + yi,(x,y \in \mathbb{Z})\) thỏa mãn: \(\left\{ {\begin{array}{*{20}{l}}{|z - 1 - i| \ge 2}\\{\left| {{z^2} - z + 1 - i} \right| \le 4}\end{array}?} \right.\)

Ta có:

\({z^2} - z + 1 - i\)\( = \left( {{z^2} - 2z + 2} \right) + (z - 1 - i)\)\( = (z - 1 - i)(z - 1 + i) + (z - 1 - i)\)\( = (z - 1 - i)(z + i)\)

Mặt khác \(\left\{ {\begin{array}{*{20}{l}}{|z - 1 - i| \ge 2}\\{\left| {{z^2} - z + 1 - i} \right| \le 4}\end{array}(*)} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{|z - 1 - i| \ge 2}\\{|(z - 1 - i)(z + i)| \le 4}\end{array}} \right.\)\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{|z - 1 - i| \ge 2}\\{|z + i| \le 2}\end{array}\quad (**)} \right.\).

Xét \(|z - 1 - i| \ge 2\) có tập hợp điểm biểu diễn số phức \(z\) là miền ngoài hình tròn (kể cả biên) \(\left( {{C_1}} \right)\) có \({I_1}(1;1),{R_1} = 2\).

Xét \(|z + i| \le 2\) có tập hợp điểm biểu diễn số phức \(z\) là miền trong hình tròn (kể cả biên) \(\left( {{C_2}} \right)\) có \({I_2}(0; - 1),{R_2} = 2\).

\( \Rightarrow \) Tát cả các điểm biểu diễn số phức \(z\) thỏa mãn \((**)\) là miền tô đậm như hình vẽ.

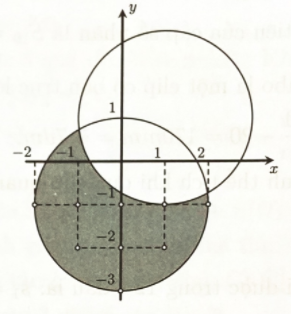
Do đó có 10 điểm có tọa độ nguyên thỏa mãn \((**)\) là:

\(( - 2; - 1),( - 1;0),( - 1; - 1),( - 1; - 2),\)\((0; - 1),(0; - 2),(0; - 3),(1; - 1),\)\((1; - 2),(2; - 1)\).

Thử lại vào điều kiện \((*)\) ta được 5 điểm thoả mãn là:

\(( - 1;0),( - 1; - 1),(0; - 1),(0; - 2),(1; - 1)\).

Vậy có tất cả 5 số phức \(z\) thỏa mãn đề bài.